I assumed from the wording of the posts before I got into this that the original poster was a beginner, didn't know a lot about this and just wanted to get started. What I originally provided in Mathematica was intended to be as simple as possible so that a beginner might be able to understand it. I carefuly and intentionally put nothing more in that than absolutely necessary. There are things that could be added that would speed it up, but with additional complexity to have to understand.
If the original question had been "I have years of experience, how can I make this go fast?" then my answer might have been very different.
Take a look at
http://mathematica.stackexchange.com/questions/104/speeding-up-this-fractal-generating-code
and see how this speeds up the process by orders of magnitude. I can understand some of that, but I have not yet been able to see how to incorporate your fractal function. Those folks are usually way beyond my skill level.
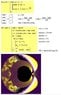
To answer your question about color, change my original simple code thus
ArrayPlot[Table[n = 0; z = a + I*b; r = z; While[Norm[r] < 3. && n < 20, r = r^z; n++]; n, {a, -3., 3., .01}, {b, -3., 3., .01}], ColorFunction ->Hue, ColorFunctionScaling -> True]
While I really hesitate to describe in "market terms", everything comes at some price. If you want to change the way a result looks you have to pay some price to accomplish that, if you want to make something faster you have to pay some price to accomplish that. The price may be small or not.
As a general rule of thumb I expect that if figuring out how to get something sort of working takes x then figuring out how to get it really exactly working precisely correctly takes between two and ten x more, getting a graphic result display that sort of shows what is going on takes another x, getting the graphics correct to show what is going on takes two to five x more and getting the graphics to be exactly precisely they way that you want them in every detail takes five to twenty x more and possibly even infinity times x more for some people.
I don't want to diminish your motivation or excitement. However you might keep this in mind. Every math operation, +,-,*,/,^ creates a bit more error. If you only do a small number of those operations then you only get a small amount of additional error. If you do lots and lots and lots of those operations you get more and more and more error. Fractal calculations do few operations in some places. Those places are almost always a single simple color. Fractal calculations do vast vast numbers of operations in some places. Those places are almost always where the complicated patterns and colors appear. Thus I propose that it is possible that almost everything about fractals is little or nothing more than a graphical display of floating point calculation error. There is a lot more that could be written to support this, but this is probably long enough already and saying anything against the myth of fractals is perhaps a lost cause anyway.