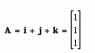You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Vectors - write ordered triples in vertical or horizontal form?
- Thread starter Outrageous
- Start date
-
- Tags
- Form Horizontal Vectors Vertical
AI Thread Summary
Vectors can be represented in both horizontal and vertical forms, with no significant difference for most practical purposes. The horizontal representation is often preferred for convenience. The discussion touches on the concepts of covariant and contravariant vectors, though the distinction is not crucial for basic applications. Advanced perspectives include the relationship between vector spaces and their duals, where row and column matrices can represent the same vectors. Ultimately, both representations are valid and can be used interchangeably in many contexts.
Mathematics news on Phys.org
tiny-tim
Science Advisor
Homework Helper
- 25,837
- 258
Hi Outrageous! 
(i'm puzzled as to why you said "complex" … you're not thinking of quaternions, are you? )
)
horizontal or vertical are both vectors
one is covariant, the other is contravariant (i can never remember which is which )
)
(i'm puzzled as to why you said "complex" … you're not thinking of quaternions, are you?
Outrageous said:A= i +j+k
A=(1,1,1)
can I write in vertical as shown?
is there any difference between them?
horizontal or vertical are both vectors
one is covariant, the other is contravariant (i can never remember which is which
 )
)for most purposes, it doesn't matter, so you might as well write everything horizontally, since that's more convenient! 

Outrageous
- 373
- 0
Thank you. That should be vector.
How to edit title?
How to edit title?
Last edited by a moderator:
tiny-tim
Science Advisor
Homework Helper
- 25,837
- 258
i don't think can edit the title 
(but you can edit the first post, to say "ignore the title!" )
)
(but you can edit the first post, to say "ignore the title!"
 )
)
Mark44
Mentor
- 38,039
- 10,520
Title changed
HallsofIvy
Science Advisor
Homework Helper
- 42,895
- 984
This is a bit more abstract and advanced but one way of looking at it is this: Given an n-dimensional vector space, V, over field F, the set of all functions from V to F, the "dual space" to V, is itself a vector space, V*, with addition defined by (f+ g)(v)= f(v)+ g(v) and (af)v= a(f(v)), also of dimenion n. We can then represent functions in V* as "row matrices" and the vectors in V as "column matrices" so that the operation f(v) is a matrix multipication.
However, because it is still true that V and V*, both being n-dimensional vector spaces, are isomorphic we can identify one with the other, the row and column matrices as both representing vectors and think of the matrix multiplication as an "inner product" on a vector space.
However, because it is still true that V and V*, both being n-dimensional vector spaces, are isomorphic we can identify one with the other, the row and column matrices as both representing vectors and think of the matrix multiplication as an "inner product" on a vector space.
Last edited by a moderator:
Outrageous
- 373
- 0
Really advanced. Thank you.
Similar threads
- Replies
- 16
- Views
- 2K
- Replies
- 25
- Views
- 6K
- Replies
- 2
- Views
- 2K
- Replies
- 10
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 8
- Views
- 2K
- Replies
- 8
- Views
- 758
- Replies
- 8
- Views
- 2K
- Replies
- 1
- Views
- 2K
Hot Threads
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math
-
B What could prove this wrong? I'm having a dispute with friends
- Started by ducknumerouno
- Replies: 94
- General Math
-
B About a definition: What is the number of terms of a polynomial P(x)?
- Started by littlemathquark
- Replies: 48
- General Math
-
B How Many Straight Lines to Connect an N by M Array of Points in a Closed Loop?
- Started by bob012345
- Replies: 25
- General Math
-
B Geometry Puzzle with 20 points in a cross pattern
- Started by bob012345
- Replies: 31
- General Math
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 25
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 5
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 11
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math