Dumbledore211
- 111
- 1
Homework Statement
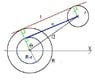
Is there any direct formula for calculating the direct common tangent of two circles without having to go all the trouble of using y-y1=m(x1-x2) to derive it for two separate tangents t1 and t2. If there is could anyone explain to me how it is derived?