Lavace
- 62
- 0
I am attempting to recreate Sutton's work on the 'Acrobot' and have modeled a good solution to the following:
http://webdocs.cs.uAlberta.ca/~sutton/book/ebook/node110.html
The physics is implemented in exactly the same way, however my particular Java implementation requires some constraint satisfaction so that particular movements cannot occur. As it stands, the Acrobot will gain momentum and then begin the second pendulum will rotate 360°. The purpose is to model a gymnast swinging on a high bar.
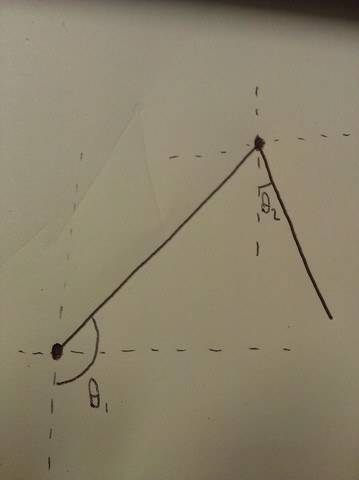
From the case figures, the two angles of the two joints are measured independently of one another. Suppose the angular velocity of the first joint is positive and starts from 0, as it revolves, the accumulated angle will eventually reach 2∏ and be reset to zero. Vice versa, a negative velocity will accumulate a negative angle until it reaches -2∏ and be reset to 0. Another point of interest is in Figure 1, θ1 is true if the ω1 >0, however if ω1 < 0 then the θ (which is already known, so we don't need this calculation, but in the context of the Figure) would be -(2π - θ1).
If you imagine the second joint as the 'hips' of an acrobat, the inner angle between the two cannot become 0. On the other hand, suppose the acrobot is vertical and the second joint has a positive velocity, it is fine for the second pendulum to continue around, but here the new angle between must not reach zero.
So, what is required are constraints that stop the inner angle becoming zero in particular scenarios. I have attempted a faulty solution that you can see below. I have also attempted to think about measuring the angle between the two, but cannot figure out a method.
I would greatly appreciate some help, as this should be simple but perhaps I am over complicating it.
Attempt:
I created multiple cases, such that if ω1 > 0 and ω2 < 0, and θ1 + θ2 > ∏ then θ2 = -(∏ - θ1). Others include using just the angles, splitting the area into spaces and solely the velocities. All of them show bugs if the acrobot suddenly changes angular velocity or goes overhead.
http://webdocs.cs.uAlberta.ca/~sutton/book/ebook/node110.html
The physics is implemented in exactly the same way, however my particular Java implementation requires some constraint satisfaction so that particular movements cannot occur. As it stands, the Acrobot will gain momentum and then begin the second pendulum will rotate 360°. The purpose is to model a gymnast swinging on a high bar.
From the case figures, the two angles of the two joints are measured independently of one another. Suppose the angular velocity of the first joint is positive and starts from 0, as it revolves, the accumulated angle will eventually reach 2∏ and be reset to zero. Vice versa, a negative velocity will accumulate a negative angle until it reaches -2∏ and be reset to 0. Another point of interest is in Figure 1, θ1 is true if the ω1 >0, however if ω1 < 0 then the θ (which is already known, so we don't need this calculation, but in the context of the Figure) would be -(2π - θ1).
If you imagine the second joint as the 'hips' of an acrobat, the inner angle between the two cannot become 0. On the other hand, suppose the acrobot is vertical and the second joint has a positive velocity, it is fine for the second pendulum to continue around, but here the new angle between must not reach zero.
So, what is required are constraints that stop the inner angle becoming zero in particular scenarios. I have attempted a faulty solution that you can see below. I have also attempted to think about measuring the angle between the two, but cannot figure out a method.
I would greatly appreciate some help, as this should be simple but perhaps I am over complicating it.
Attempt:
I created multiple cases, such that if ω1 > 0 and ω2 < 0, and θ1 + θ2 > ∏ then θ2 = -(∏ - θ1). Others include using just the angles, splitting the area into spaces and solely the velocities. All of them show bugs if the acrobot suddenly changes angular velocity or goes overhead.