baby_1
- 159
- 16
Hello
I have some question that i confused to know them
1-what is difference between Vector and Line in 3D and 2D?
2-how can find the vertical vector on a surface or line?
3-how can find the angle between two vector or line only with their size?( i do it with Inner Product equation but without the Inner Product value how can do that
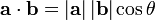
?)
Thanks
I have some question that i confused to know them
1-what is difference between Vector and Line in 3D and 2D?
2-how can find the vertical vector on a surface or line?
3-how can find the angle between two vector or line only with their size?( i do it with Inner Product equation but without the Inner Product value how can do that
?)
Thanks