1plus1is10
- 51
- 0
Hello everyone,
The sum of two sine waves that have close frequencies can produce an Envelope Wave:
http://en.wikipedia.org/wiki/Envelope_(waves)
What formula can I use to turn it into one wave (i.e. one frequency and amplitude)?
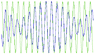
Example pic attached:
The blue "Envelope Wave" is actually 2 sine waves combined.
And the green sine wave is what I really want.
Finally, I am curious to know the proper keywords that would have allowed me to find this formula on Google, or are there not any?
Thank-you very much.
The sum of two sine waves that have close frequencies can produce an Envelope Wave:
http://en.wikipedia.org/wiki/Envelope_(waves)
What formula can I use to turn it into one wave (i.e. one frequency and amplitude)?
Example pic attached:
The blue "Envelope Wave" is actually 2 sine waves combined.
And the green sine wave is what I really want.
Finally, I am curious to know the proper keywords that would have allowed me to find this formula on Google, or are there not any?
Thank-you very much.