MathewsMD
- 430
- 7
If the gymnast has a mass, m = 36.7 kg, and the angle θ = 4.0°, calculate the tension in the rope from which she is hanging.
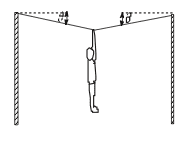
ƩFx = T1x - T2x = 0
Then T1cos4 = T2cos4
T1 = T2 = T
ƩFy = 2Ty - mg
2Tsin4 = mg
T = mg/2sin4 = 2578 N
I have gotten the solution. I am just confused at one part. Do we analyze the tension in the string on each side of the gymnast separately, then add them together? Or, do we just find the tension on one side and that is it (like my solution)?
I am just confused since I remember learning tension in a massless rope is considered to be uniform, but if there is a force being applied to a part of it (this time in the middle) I don't know if we're supposed to analyze tension together or not since it is essentially a node and I considered it like I would two separate strings in my solution.
Also, if the gymnast was not in the middle of the string (i.e. θ1 = 6.0° and θ2 = 10.0°) how would this change the situation and the resultant tension in the rope. Would it have any effect?
Any help would be greatly appreciated!
ƩFx = T1x - T2x = 0
Then T1cos4 = T2cos4
T1 = T2 = T
ƩFy = 2Ty - mg
2Tsin4 = mg
T = mg/2sin4 = 2578 N
I have gotten the solution. I am just confused at one part. Do we analyze the tension in the string on each side of the gymnast separately, then add them together? Or, do we just find the tension on one side and that is it (like my solution)?
I am just confused since I remember learning tension in a massless rope is considered to be uniform, but if there is a force being applied to a part of it (this time in the middle) I don't know if we're supposed to analyze tension together or not since it is essentially a node and I considered it like I would two separate strings in my solution.
Also, if the gymnast was not in the middle of the string (i.e. θ1 = 6.0° and θ2 = 10.0°) how would this change the situation and the resultant tension in the rope. Would it have any effect?
Any help would be greatly appreciated!