jrand26
- 11
- 0
Hi all, I'm working on designing a variable inductor using a ferrite core. The basic idea is that I have a large wound inductor on the central arm which I pass a DC-current through, and a smaller, variable inductor on one of the side arms. As you increase the current through the main winding, the inductance on the side arm decreases. Am I correct in saying that this is due to a drop in permeability in the core? As per the equation,
L = \frac{\mu N^2 A}{l}
What is the physical explanation for an increased current causing a decrease in permeability in the core? Image 1 shows something similar, except I'm only using one of the side arms and there is no air gap on the central winding.
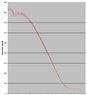
While the design essentially works I'm not satisfied with the accuracy. The biggest problem I've been having is that when I repeat my measurements I get quite a spread of results, which I find really interesting (image 2 shows the curve bounded by max/min measurements). Is there something about the physics of the core which makes it inherently difficult to control? I have noticed hysteresis but I'm not sure that it should effect repeatability. I'm also unsure of the shape of the curve, why does the inductance increase with increasing current briefly at the start?
Any help/comments or links to other resources appreciated :)
L = \frac{\mu N^2 A}{l}
What is the physical explanation for an increased current causing a decrease in permeability in the core? Image 1 shows something similar, except I'm only using one of the side arms and there is no air gap on the central winding.
While the design essentially works I'm not satisfied with the accuracy. The biggest problem I've been having is that when I repeat my measurements I get quite a spread of results, which I find really interesting (image 2 shows the curve bounded by max/min measurements). Is there something about the physics of the core which makes it inherently difficult to control? I have noticed hysteresis but I'm not sure that it should effect repeatability. I'm also unsure of the shape of the curve, why does the inductance increase with increasing current briefly at the start?
Any help/comments or links to other resources appreciated :)