P3X-018
- 144
- 0
Homework Statement
(See the attachment)
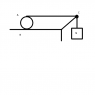
A thin string has been wound around a homogeneuos circular disk A in such a way that the disk can roll on a horizontal surface. The mass of the disk is M, and has radius R. The string goes around a small frictionless pulley C at a height 2R above te horizental table B. To the free end of the string a bob of mass M is attached.
It is further assumed that the coefficient of friction \mu is so large that the disk rolls without slipping on the horizontal table.
1. Determine the magnitude of the force S, with which the string acts on the disk as long as the system moves under the influence of gravity.
2. Determine the smallest value of \mu that permits the disk to roll without slipping.
The Attempt at a Solution
The way I tried solving the first problem, is to first write down the equation of motion of the bob, as
M\ddot{y} = Mg-S
And the equation of motion for rotation
I_{CM}\ddot{\theta} = RS + Rf
where f is the force of friction on the disk providing a torque in the same direction as the strong force S.
Since the string is considered taut throughout the motion we can use the relation between the acceleration and angular acceleration, \ddot{y} = R\ddot{\theta}. When I solve for the string force, by using that I_{CM} = MR^2/2 I get
S = \frac{1}{3}(Mg - 2f)
But this result looks wrong, because the string force would be negative if the friction force is f > Mg/2.
Shouldn't a "negative" string force appear when if the frictional force was smaller than some given value, which would imply that disk would slip?
So the equations of motion must be wrong. Any hint to what I do wrong?