A simple movable pulley not at equilibrium

AI Thread Summary
In a movable pulley system, pulling harder than the equilibrium force (half the weight of the object) results in the weight accelerating upwards. The tension in the rope remains uniform and equals the weight of the object (mg) when the pulling force equals the object's weight. This creates a total upward force of 2mg, leading to an acceleration of g for the weight. The discussion clarifies that understanding pulleys outside of equilibrium involves applying Newton's second law to analyze forces and accelerations. The conclusion confirms that the described behavior and calculations are accurate.
DocZaius
Messages
365
Reaction score
11
Note: This is not a homework question. I have constructed this question to help me understand a concept.

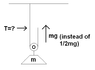
If I have an object hanging off a single (frictionless, negligible mass) movable pulley, the equilibrium system entails me pulling on the free end of the (frictionless, negligible mass) rope with half as much force as the object weighs.

What happens if I pull harder than that?

See the attached GIF. What would be the behavior of the weight? Would it accelerate up? If so, at what acceleration? What would be the tension in the left side of the rope?

Every resource I have access to that mentions pulleys keeps talking about pulleys in this type of setup in equilibrium. I am interested in furthering my understanding in regards to pulleys not in equilibrium.

Thank you for any help.
 

Attachments

  • pulley.GIF
    pulley.GIF
    2.9 KB · Views: 910
Last edited:
Physics news on Phys.org
The tension is uniform throughout the rope. The upward force on the pulley/mass will equal twice the tension. To find the acceleration, just add the vertical forces and apply Newton's 2nd law.
 
So me increasing my pulling force from an equilibrium inducing (1/2)mg to mg will cause the rope to have a uniform tension of mg, thus making the total upward force 2mg (the tension of the rope being a uniform "mg"). This accelerate the weight, which weighs mg, upwards at acceleration = g.

Is that correct?
 
Yes, that's correct.
 

Thread 'Is calling fictitious forces not real just about terminology?'

Hi there, im studying nanoscience at the university in Basel. Today I looked at the topic of intertial and non-inertial reference frames and the existence of fictitious forces. I understand that you call forces real in physics if they appear in interplay. Meaning that a force is real when there is the "actio" partner to the "reactio" partner. If this condition is not satisfied the force is not real. I also understand that if you specifically look at non-inertial reference frames you can...
View full post »

Thread 'Derivation of Hamilton's Principle: Questions'

I have recently been really interested in the derivation of Hamiltons Principle. On my research I found that with the term ##m \cdot \frac{d}{dt} (\frac{dr}{dt} \cdot \delta r) = 0## (1) one may derivate ##\delta \int (T - V) dt = 0## (2). The derivation itself I understood quiet good, but what I don't understand is where the equation (1) came from, because in my research it was just given and not derived from anywhere. Does anybody know where (1) comes from or why from it the...
View full post »

Similar threads

Why are these pulleys equivalent?
Replies
16
Views
1K
1 pulley with mass, 1 mass on the cord, 1 external force, no gravity
Replies
16
Views
3K
Accelerating motion with a pulley
Replies
10
Views
2K
Distance Traveled by an object on a pulley
Replies
17
Views
5K
Pulley Carrying Capacity: Can It Handle 150 lbs?
Replies
9
Views
3K
How Does the Distance y Change When Mass x Varies in a Pulley System?
Replies
5
Views
3K
Moment of Inertia of Massless Pulley w/String & Mass m Attached
Replies
14
Views
3K
Problem with pulleys - two fixed and one movable
Replies
22
Views
374
Mass Pulley and torque -- Confusion in this Atwood machine problem
Replies
11
Views
972
Why Does Pulley Require Less Work to Lift Mass?
Replies
6
Views
7K

Hot Threads

Recent Insights

Back
Top