Pressure Difference in Test Tube w/ Air Flow Rate

[iki08]

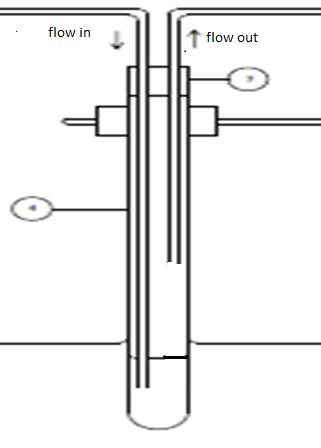
lets say if i have a test tube (diameter 3cm and height 30cm) seal with a rubber. in the test tube there 100ml of water = around 10 cm height. if air was flow into the test tube with flow rate around 20L/min, and after a few sec, the rubber was push out. in general i understand that the pressure inside the test tube is higher than atmospheric pressure. but i can't find any mathematical solution that relate flow rate and pressure to proof that the pressure inside the test tube is higher than outside. can anyone explain it to me.

 

[asdofindia]

What's that flow out doing there in the diagram?
If air doesn't flow out at the same rate, it's obvious that the pressure inside increases.

If it IS flowing out at the same rate, it may be that the bubbling in the water causes some of the water molecules to come out of the liquid, and increase the pressure over the surface in the test tube

 

[rcgldr]

I'm not sure the water does much other than resist the flow on the inlet tube. If the tube were to remain sealed, and assuming the outlet tube exits into the atmoshpere, then the outlet tube's resistance to flow is the primary reason pressure inside the tube would be greater than the ambient pressure out side. The pressure on the inlet tube would have to be greater still in order to overcome the resistance in the water so that the air exits the water at the same pressure as the pressure inside the tube.

You could simplify this quite a bit by simply having a long length of pipe with one end connected to a pump and the other end exiting to the atmoshpere. The pressure at the pump end would be higher than the pressure at the exit end.

http://en.wikipedia.org/wiki/Darcy–Weisbach_equation

http://en.wikipedia.org/wiki/Head_loss#Head_loss

 

[iki08]

sorry for the late reply

asdofindia - air was flow to the tube to mix the reactant in the tube then the 'flow out' is for air to flow out to atm and the outside flow rate is around 38 L/min. i just don't know which equation i should use to solve this problem.rcgldr- are you sure the darcy weisbach equation can be applied to this problem? i thought that equation only can be used for liquid. and usually what is the darcy friction factor value of rubber/vinyl tubing?

 

[rcgldr]

rcgldr- are you sure the darcy weisbach equation can be applied to this problem?

No, but it may be possible to find "head loss" information for air and certain common types of tubing or pipes. I don't know how much pressure a glass test tube can handle, so if you wanted to measure the pressure on a sealed test tube, I'd recommend getting a stronger tube.