keysle
- 4
- 0
What's it called when a 3D shape can be made of 2D surfaces of all the same shape and dimensions?
To make a cube, I can use 6 4-sided-squares (of course they're 4 sided)
To make a pyramid (3 sided), I can use 4 3-sided-triangles
I can do this with pentagon as well (i don't know what the shape is called)
Eventually I can't do this as the sides of the shape increase because the remaining angle.
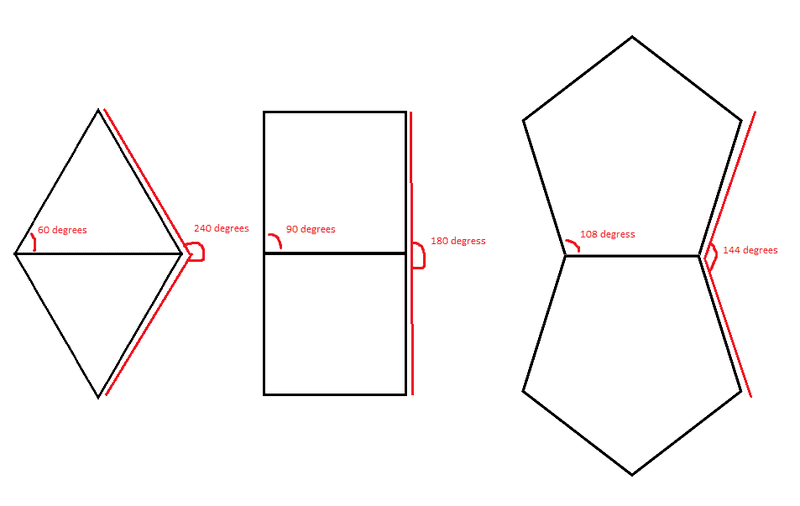
... after some thinking I realized I can only do this with 3 equilateral shapes.
3 sided
4 sided
and 5 sided
Once I get to the hexagon ... well
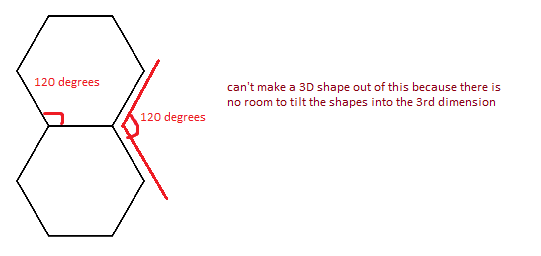
Now here's an even more interesting question: Are there any others shapes convex or concave equilateral or not that can be used to create a 3D shape? (where the base shapes remains the same)
If so how can one determine if a shape is capable of doing this?
To make a cube, I can use 6 4-sided-squares (of course they're 4 sided)
To make a pyramid (3 sided), I can use 4 3-sided-triangles
I can do this with pentagon as well (i don't know what the shape is called)
Eventually I can't do this as the sides of the shape increase because the remaining angle.
... after some thinking I realized I can only do this with 3 equilateral shapes.
3 sided
4 sided
and 5 sided
Once I get to the hexagon ... well
Now here's an even more interesting question: Are there any others shapes convex or concave equilateral or not that can be used to create a 3D shape? (where the base shapes remains the same)
If so how can one determine if a shape is capable of doing this?