misunderstanding time dilation and length contraction

Gavroy

hi

sorry about my english. i am from france.
i have a few questions about the image i have found in my schoolbook that i attached to this post.

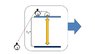
there is a light signal moving up and down and each time it reaches the upper mirror this is somehow detected. there are also two observers: one standing outside(oberserver 1) and one moving with the system and now my textbook says that no matter whether this thing is moving horizontal(as the arrow shows) or vertical(not shown in this picture) to the oberserver standing outside, this guy would detect the same click rate, but i highly doubt it.

let me start with the observer moving with the aperature. he is the one who measures no time dilation as he is moving with the system and measures no length contraction, so the time he waites for a click is t=2l/c where l is the length of this thing.

while the oberserver standing outside will measure a time dilation when the aperature is moving horizontal to him.
that means that he is just waiting: t=2l/c*(1-v^2/c^2)^(1/2) for a click.

WHILE

if the aperature is also moving vertical than there will also be a length contraction and therefore: t=2l/c as both square roots cancel out.

but where am i wrong?

Attached Thumbnails

 

Doc Al

You forgot to take into account that the apparatus moves during the clock tick. So the distance traveled by the light is not simply twice the contracted length between the mirrors.

phinds

perhaps this will be more clear:

www.phinds.com/time dilation