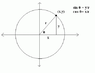
Yes, as hypermorphism stated, the definitions of cosine and sine are not really about right trianges: they're about rotation. Now, you know that the argument of sin and cos are angles, correct (for your purposes, of course)? That is, they take in an angle and spit out a "regular" value.
Now, imagine that you have a coordinate plane. You construct that angle you want at the origin and draw a ray that comes out of it. At some point, it will intersect a circle with an arbitrary radius r. Now, imagine that you take that point, and find its coordinates. Call them (x,y). Sine is defined to be the y coordinate divided by the radius of the circle, and cosine is defined to be the x coordinate divided by the radius. (See the attached picture for clarification). What does that mean for us? Since we can draw an angle of any size we want, sin and cos can be defined for any angle, not just the angles between 0 and 90 degrees! We can find the sine of, -10 degrees, 270 degrees, whatever: it doesn't matter.
Anyway, you might be wondering, "So, how does this apply to what I though cos was, adjacent over hypotenuse?" Take a closer look at the picture I drew. Imagine that you were only considering the angles in the first quadrant, i.e., when they are between 0 and 90 degrees. Cosine would be defined to be x/r. However, if you think about it, every coordinate on the plane can have a line dropped down from it, to the x-axis. This forms a right triangle, with legs of length x and y and hypotenuse of length r. Can you see where I'm going with this? The leg closest to the angle, the "adjacent" one, has length x. The hypotenuse has length r. Therefore, adjacent/hypotenuse = x/r.
Now, back to your original question. From the picture provided, it's obvious that the ray drawn at 90 degrees intersects the circle on the y-axis. Therefore, the coordinates of the intersection point are (0,r) (where r is the radius of the circle again). Thus, x=0, and cos(90 degrees) = x/r = 0/r = 0.