baby_1
- 159
- 16
Hello
Im solving a problem with calculator to find the zeta in this equation
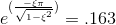
but as i see some persons they solved this equation with different numbers(1.63 ) without calculator.now i want to know
how can fine zeta in this equation without calculator and fast?
Im solving a problem with calculator to find the zeta in this equation
but as i see some persons they solved this equation with different numbers(1.63 ) without calculator.now i want to know
how can fine zeta in this equation without calculator and fast?
Last edited by a moderator: