Jano L. said:
One important definition of polarization which was not mentioned so far is that it is the total electric dipole moment of neutral set of molecules divided by the volume they occupy, or, which is the same thing, number density of molecules times their average dipole moment:
$$
\mathbf P = \mathscr{N} \langle \boldsymbol \mu \rangle
$$
This applies well to dielectric media (the definition is unambiguous).
In case the medium is conducting, like metals, this concept of polarization does not apply, because there are no neutral molecules.
For me this is the most intuitive way to understand this. Hopefuly the OP has learned about simple electic dipoles. Here is the way I think of it:
First a definition. If you have a charge +q and a charge -q, separated by \mathbf{d} (a vector that starts at -q and ends at +q) then the dipole moment is \mathbf{p} = q \mathbf{d}. Now when we consider a dielectric media, there are molecules that become distorted when an external field is applied, and the distortion can be modeled by a dipole.
If we look on a microscopic scale, the field and dipoles make a rapidly varying (in the spatial sense) electric field in the vicinity of each molecule, in fact we usually do not care about the fluctuations on these tiny scale sizes. Instead, we are usually interested in macroscopic behavior. So one approach is to average the fields, and the polarization vectors, over volumes that contain many of the elementary dipoles and yield (approximately) continuous vector fields, but are still small enough volumes so that the scale sizes we typically are interested in are preserved. When we do this, we obtain what are usually called the
macroscopic Maxwell equations. The terms associated with the dielectric media involve this average polarization density,
<br />
\mathbf{P}(\mathbf{r}) = \frac{1}{\Delta V} \sum_{\mathbf{r}_i \, in\, \mathbf{r}+\Delta V} \mathbf{p}(\mathbf{r}_i) <br />
Note that due to the sign convention for electric dipoles, \nabla \cdot \mathbf{P} = -\rho_b where I have let \rho_b represent bound charge density. There is nothing fictitious about these charges, they are really there. To convince yourself of the sign, consider a bunch of elementary dipoles all with their -q charges at the origin (say), and all of the \mathbf{d} vectors pointing radially outward. Clearly this configuration has positive divergence at the the origin, where there is a bunch of negative charges.
Also, \frac{\partial \mathbf{P}}{\partial t} represents a current. To understand this think about a single dipole. if the time derivative is positive, it means either the charges are increasing (meaning positive charge must be moving from the -q location to the +q location) or the vector \mathbf{d} is increasing, which simply means (for example) the +q charge is moving away from the -q charge, so is a positive current.
Hence, to include dielectric media into our
macroscopic Maxwells equations (again, where we usually think of all quantities as having been averaged) we obtain,
<br />
\begin{eqnarray}<br />
\nabla \cdot \epsilon_0 \mathbf{E} & = & \rho - \nabla \cdot \mathbf{P}. \\<br />
\nabla \times \mu_0^{-1} \mathbf{B} & = & \mathbf{J} + \frac{\partial }{\partial t}\epsilon_0 \mathbf{E} + \frac{\partial }{\partial t} \mathbf{P}. <br />
\end{eqnarray}<br />
If we define \mathbf{D} = \epsilon_0 \mathbf{E} + \mathbf{P} then these become the more familiar,
<br />
\begin{eqnarray}<br />
\nabla \cdot \mathbf{D} & = & \rho. \\<br />
\nabla \times \mu_0^{-1} \mathbf{B} & = & \mathbf{J} + \frac{\partial }{\partial t} \mathbf{D}. <br />
\end{eqnarray}<br />
I hope that helps a little!
jason
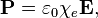Can somebody explain to me why exactly this is so? My book just says that's how polarization is defined.. Can you guys give me an intuitive understanding of why? Only thing I know is that χ is related to κ, the dielectric constant, and κ is related to how well a dielectric polarizes.
