joao_pimentel
- 68
- 0
Hello
I was patent examiner on the Portuguese patent office for 3 years and we have a lot of perpetua mobile applications, so I wanted to find now, the theoretical misunderstanding I'm missing here

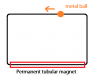
Imagine you have a track (on a table, on the xOy plane) on which a metal ball would follow, and at a certain length of the track, there would be a tubular permanent magnet, that would create a force on the ball accelerating it. That ball would be accelerated every time it passes through the tube!
I know that there is some paradox on my lemma, but I can't find where
Thank you in advance
PS: Actually I know that the magnetic field is conservative, but something is missing
I was patent examiner on the Portuguese patent office for 3 years and we have a lot of perpetua mobile applications, so I wanted to find now, the theoretical misunderstanding I'm missing here
Imagine you have a track (on a table, on the xOy plane) on which a metal ball would follow, and at a certain length of the track, there would be a tubular permanent magnet, that would create a force on the ball accelerating it. That ball would be accelerated every time it passes through the tube!
I know that there is some paradox on my lemma, but I can't find where
Thank you in advance
PS: Actually I know that the magnetic field is conservative, but something is missing