How Do Accelerations and Angular Acceleration Relate in a Disk and Mass System?

[Saitama]

Homework Statement

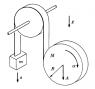
A disk of mass M and radius R unwinds from a tape wrapped around it. The tape passes over a frictionless pulley, and a mass m is suspended from the other end. Assume that the disk drops vertically.

a. Relate the accelerations of m and the disk, a and A, respectively to the angular acceleration of disk.

b. Find a, A and $\alpha$.

Homework Equations

The Attempt at a Solution

Applying Newton's second law on disk: $Mg-T=MA$ where T is the tension in tape.

For m: $mg-T=ma$. I still need one more equation.

I am not sure but do I have to equate the acceleration along string? For instance, the point in contact with disk has acceleration $A-\alpha R$. Does this mean, $a=A-\alpha R$?

Any help is appreciated. Thanks!

 

[haruspex]

Does this mean, $a=A-\alpha R$?

That's about right, but be careful with the signs. Which way are you defining as positive for each variable?

 

[Saitama]

That's about right, but be careful with the signs. Which way are you defining as positive for each variable?

I am defining downward to be positive (the direction of g). But I still don't see why there is a sign error in my equation.

 

[haruspex]

I am defining downward to be positive (the direction of g). But I still don't see why there is a sign error in my equation.

There's also the question of which direction of rotation is positive. Taking that to be clockwise in the diagram, I have no problem with the A-αR part. But remember that a is upwards on this side of the pulley. E.g. suppose A=0. A positive a for the descending mass should produce a positive α, but in your equation it gives negative α.

 

[Saitama]

There's also the question of which direction of rotation is positive. Taking that to be clockwise in the diagram, I have no problem with the A-αR part. But remember that a is upwards on this side of the pulley. E.g. suppose A=0. A positive a for the descending mass should produce a positive α, but in your equation it gives negative α.

So that means, $a=-A+\alpha R$? This also looks incorrect to me. The clue for the answer states that if A=2a, then $\alpha=3A/R$ but if I substitute a=A/2, I get $\alpha=3A/(2R)$.

 

[haruspex]

So that means, $a=-A+\alpha R$? ... if I substitute a=A/2, I get $\alpha=3A/(2R)$.

That's not what I get with that substitution. You might be mixing up your A and a.

 

[Saitama]

That's not what I get with that substitution. You might be mixing up your A and a.

I don't see what I did wrong. Given clue: $A=2a \Rightarrow a=A/2$. Plugging this in $a=-A+\alpha R$, $A/2=-A+\alpha R \Rightarrow 3A/2=\alpha R$. Is something wrong with my expression? I have tried to make the equations according to the diagram. Please tell me if something is unclear.

 

[Enigman]

Try to use the length (or the change in length) of the tape for another constraint.

 

[haruspex]

I don't see what I did wrong. Given clue: $A=2a \Rightarrow a=A/2$. Plugging this in $a=-A+\alpha R$, $A/2=-A+\alpha R \Rightarrow 3A/2=\alpha R$. Is something wrong with my expression? I have tried to make the equations according to the diagram. Please tell me if something is unclear.

Oh, sorry - it's me that's getting my A and a confused. Anyway, I insist that A+a = αR. Consider two special case: if m is held still then a = 0 and A = αR; likewise if the centre of M is held fixed than A=0 and a = αR.

 

[Saitama]

Oh, sorry - it's me that's getting my A and a confused. Anyway, I insist that A+a = αR. Consider two special case: if m is held still then a = 0 and A = αR; likewise if the centre of M is held fixed than A=0 and a = αR.

Umm...what do I have to do after considering these two cases? I still don't get the right $\alpha$ after substituting a=A/2.

 

[Enigman]

Try to use the length (or the change in length) of the tape for another constraint.

Let length be L(t)
$\frac{d^2 L}{dt^2}=?$
How does that ^ relate to α? What about a and A?
:zzz:^{need sleepzzz...}

 

[Tanya Sharma]

Hi Pranav...

Please write down all the equations you have formed.Somehow I am not able to follow.

 

[Saitama]

Let length be L(t)
$\frac{d^2 L}{dt^2}=?$
How does that ^ relate to α? What about a and A?
:zzz:^{need sleepzzz...}

Hi Enigman!

I am honestly lost at finding out the expression for L(t).

Let $L_0$ be the initial length of tape. If the block moves down x and the disk moves down y, the new length of string is:

$$L(t)=L_0+x+y$$

Differentiating wrt time twice,

$$\frac{d^2L}{dt^2}=a+A-\alpha R$$.

What should I do with this?

Hi Pranav...

Please write down all the equations you have formed.Somehow I am not able to follow.

Hi Tanya!

Here are the equations I wrote before this post:
For disk: $Mg-T=MA$
For block: $mg-T=ma$

Relating the accelerations: $a=-A+\alpha R$.

The above equations are written with reference to the attached diagram in #1.

 

[Tanya Sharma]

Hi Tanya!

Here are the equations I wrote before this post:
For disk: $Mg-T=MA$
For block: $mg-T=ma$

Relating the accelerations: $a=-A+\alpha R$.

The above equations are written with reference to the attached diagram in #1.

Good...These are correct equations .Now what is the problem ?

 

[Saitama]

Good...These are correct equations .Now what is the problem ?

The problem is that these equations do not satisfy the given clue for part a. I quote the clue from the book:

If $A=2a$, then $\alpha =3A/R$

What I have is $a=-A+\alpha R$. Substituting a=A/2, $\alpha = 3A/(2R)$ which is incorrect. But if I substitute A=2a, I get $\alpha =3a/R$. Error in the book I guess?

 

[Tanya Sharma]

The problem is that these equations do not satisfy the given clue for part a. I quote the clue from the book:

What I have is $a=-A+\alpha R$. Substituting a=A/2, $\alpha = 3A/(2R)$ which is incorrect. But if I substitute A=2a, I get $\alpha =3a/R$. Error in the book I guess?

$\alpha =3a/R$ is correct

 

[Saitama]

Thanks haruspex, Tanya and Engiman! :)

@Tanya: Can you please confirm if my expression for d^2L/dt^2 is correct? Also, what am I supposed to do with that? Equate it to zero?

 

[Tanya Sharma]

@Tanya: Can you please confirm if my expression for d^2L/dt^2 is correct? Also, what am I supposed to do with that? Equate it to zero?

Why are you doing all this ? This isn't required .

 

[Saitama]

Why are you doing all this ? This isn't required .

Since I have written it down, I would like to know if it's valid or not.

 

[Tanya Sharma]

Since I have written it down, I would like to know if it's valid or not.

No...that's wrong .

What does the term d²L/dt² represent ?

 

[Saitama]

What does the term d²L/dt² represent ?

The rate of change of rate of change of length of the tape.

Honestly, I don't know how to interpret it. dL/dt is the rate at which the length of string changes. I don't see how should I interpret the second derivative. :(

 

[Tanya Sharma]

d²L/dt² = αR

Now, L = L₀+x+y

Differentiating twice, d²L/dt² = a+A

and αR = a+A

 

[Saitama]

d²L/dt² = αR

Now, L = L₀+x+y

Differentiating twice, d²L/dt² = a+A

and αR = a+A

Ah yes, thanks a lot Tanya!

 

[Tanya Sharma]

You are welcome