Bashyboy
- 1,419
- 5
Homework Statement
Hello, I am working on a problem involves my using the Euler Method to approximate the differential equation \displaystyle \frac{df}{dt} = af(t) - b[f(t)]^2, both when b=0 and when b is not zero; and I am to compare the analytic solution to the approximate solution when b=0.
Homework Equations
The Attempt at a Solution
Here is my code
Code:
f(1) = 1000;
t(1)= 0;
a = 10;
b = 0 ;
dt = 0.01;
Nsteps = 10/dt;
for i = 2:Nsteps
t(i) = dt + t(i-1);
%f(i) = f(i-1)*(1 + dt*(a - b*f(i-1)));
f(i) = f(i-1)*(1 + a*dt);
end
plot(t,f,'r-')
hold on
fa= a*exp(a*t)
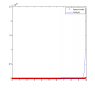
plot(t,fa,'bo')When b=0, the solution to the differential equation is f(t) = c e^{at}. When I apply the initial condition, that f(0) = 1000, then the differential equation becomes f(t) = 1000 e^{at}. Now, my professor said that a differential equation has an analytic solution, no matter what time step you use, the graph of analytic solution and the approximation (Euler's Method) will coincide. So, I expected the two graphs to overlap. I attached a picture of what I got.
Why did this occur? In order to get the graphs to overlap, I changed 1000 to 10, which is a, just for the heck of it. When I did this, the two overlapped. I don't understand. What am I doing incorrectly?