Inequality Definition and 1000 Threads
-
A
Graduate Derivation of the CHSH inequality
Bell's 1971 derivation The following is based on page 37 of Bell's Speakable and Unspeakable (Bell, 1971), the main change being to use the symbol ‘E’ instead of ‘P’ for the expected value of the quantum correlation. This avoids any implication that the quantum correlation is itself a...- Alien8
- Thread
- Chsh Derivation Inequality
- Replies: 63
- Forum: Quantum Physics
-
R
MHB Elementary proof of generalized power mean inequality
This is problem 20b from chapter I 4.10 of Apostol's Calculus I. The geometric mean $$G$$ of $$n$$ positive real numbers $$x_1,\ldots, x_n$$ is defined by the formula $$G=(x_1x_2\ldots x_n)^{1/n}$$. Let $$p$$ and $$q$$ be integers, $$q<0<p$$. From part (a) deduce that $$M_q<G<M_p$$ when... -
T
MHB How do I solve an inequality with a quadratic function?
Hello, I have this inequality: $$-x^2 + 4 < 0$$ Then, I get to $$-(x-2)(x+2) < 0$$ Now, how do I solve this question from here. I understand that x = -2, or x =2 but how do I use this to solve the inequality? Thanks- tmt1
- Thread
- Inequality
- Replies: 7
- Forum: General Math
-
T
MHB Therefore, the solution set is $\boxed{ \left[ -4, 2 \right] }$.
Solve the Ineqality $$x^2 + 2x -8 \le 0$$I know enough to factor it like this $$(x-4) (x+2) \le 0$$ So I get 4 and -2. I just don't know how to get to the answer from here which is: $$x \ge -4\cup x\le 2$$ unless I'm misreading the answer incorrectly. Thanks- tmt1
- Thread
- Inequality
- Replies: 2
- Forum: General Math
-
P
Prove Inequality n! > n^3 for n > 5 w/ M.I.
Homework Statement Use M.I. to prove that n! > n^3 for n > 5 The Attempt at a Solution I already proved n! > n^2 for n>4, but this is nothing like that. This is my inductive step so far. n=k+1 (k+1)! > (k+1)^3 (k+1)! - (k+1)^3 > 0[/B] (k+1)! - (k+1)^3 = (k+1)[k! - (k+1)^2]...- Panphobia
- Thread
- Inequality Proof
- Replies: 12
- Forum: Precalculus Mathematics Homework Help
-
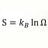
Graduate Disconnect With Inequality Realism Assumption And Bells' Lambda
Bell, QM Ideas - Science 177 1972 :" Strictly, however. a hidden variable theory could be non-deterministic; the hidden variable could evolve randomly (possibly even discontinuously) so that their values at one instant do not specify their values at the next instant" From the locality...- morrobay
- Thread
- bells Inequality Lambda Realism
- Replies: 1
- Forum: Quantum Physics
-
J
Undergrad The triangle inequality in CHSH, where is the triangle?
http://en.wikipedia.org/wiki/CHSH_inequality#Bell.27s_1971_derivation The last step of the CHSH inequality derivation is to apply the triangle inequality. I see there are relative polarization angles, but I don't see any sides have defined length to make up a triangle. Where is the triangle?- johana
- Thread
- Chsh Inequality Triangle Triangle inequality
- Replies: 5
- Forum: Quantum Physics
-

MHB Is $\sin^2 x$ Less Than $\sin x^2$ for $0 \leq x \leq \sqrt{\frac{\pi}{2}}$?
Hi MHB, When I first saw the problem (Prove that $\sin^2 x<\sin x^2$ for $0\le x\le \sqrt{\dfrac{\pi}{2}}$), I could tell that is one very good problem, but, a good problem usually indicates it is also a very difficult problem and after a few trials using calculus + trigonometry method, I... -

MHB Inequality Challenge X: Prove $\ge 3l-4m+n$
There are real numbers $l,\,m,\,n$ such that $l\ge m\ge n >0$. Prove that $\dfrac{l^2-m^2}{n}+\dfrac{n^2-m^2}{l}+\dfrac{l^2-n^2}{m}\ge 3l-4m+n$.- anemone
- Thread
- Challenge Inequality
- Replies: 2
- Forum: General Math
-

MHB Proving an Inequality Involving Real Numbers
If $a,b\in \mathbb{R}^{+}.$ Show that $a>b\implies a^{-1}<b^{-1}.$- Julio1
- Thread
- Inequality Numbers Real numbers
- Replies: 3
- Forum: Topology and Analysis
-
E
Graduate Bell's Inequality Explanation for Intelligent Non-Scientist
I have literally spent all day reading and am still very much in the dark. First off does anyone have a link to detailed blow by blow account that doesn't assume an understanding of advanced maths and physics concepts and notations but will actually address the issue in depth? Here are...- ep1987
- Thread
- Explanation Inequality
- Replies: 41
- Forum: Quantum Physics
-

MHB Integral Inequality: Prove $\left|f\left(\frac{1}{2}\right)\right|$ Bound
Here's my first challenge! Let $f : [0,1] \to \Bbb R$ be continuously differentiable. Show that $\displaystyle \left|f\left(\frac{1}{2}\right)\right| \le \int_0^1 |f(t)|\, dt + \frac{1}{2}\int_0^1 |f'(t)|\, dt$. -
M
Solve Rational Inequality: Find Integer Roots [-2, 3]
Homework Statement Find all integer roots that satisfy (3x + 1)/(x - 4) < 1. The Attempt at a Solution I would do this: Make it an equation and find x such that (3x + 1)/(x - 4) = 1. 3x + 1 = x - 4 2x = -5 x = -5/2 Then check if the inequality is valid for values smaller than x and for...- mafagafo
- Thread
- Inequality Rational
- Replies: 7
- Forum: Precalculus Mathematics Homework Help
-
L
Graduate Is There a Connection Between Inequality and the Unit Disc?
hi there, I am trying to prove the following inequality: let z\in \mathbb{D} then \left| \frac{z}{\lambda} +1-\frac{1}{\lambda}\right|<1 if and only if \lambda\geq1. The direction if \lambda>1 is pretty easy, but I am wondering about the other direction. Thanks in advance- Likemath2014
- Thread
- Disc Inequality Unit
- Replies: 20
- Forum: Topology and Analysis
-
A
Inequality - Proof that √(a^2)<√(b^2) does not imply a<b
Hi everyone! First of all thank you for a great forum! I downloaded the app and find it ingenious! The problem stated above is from "3000 Solved Problems in Calculus". The book solves this problem simply by stating: "No. Let a=1 and b=-2". However, I am curious to know if it is possible...- Akitirija
- Thread
- Inequality Proof
- Replies: 4
- Forum: Precalculus Mathematics Homework Help
-
R
MHB Show that equality holds in Cauchy-Schwarz inequality if and only if....
This is from section I 4.9 of Apostol's Calculus Volume 1. The book states the Cauchy-Schwarz inequality as follows: $$\left(\sum_{k=1}^na_kb_k\right)^2\leq\left(\sum_{k=1}^na_k^2\right)\left(\sum_{k=1}^nb_k^2\right)$$ Then it asks you to show that equality holds in the above if and only if... -
C
Undergrad Looking for counterexample in inequality proof
Hi guys, I have to teach inequality proofs and am looking for an opinion on something. Lets say I have to prove that a2+b2≥2ab. (a very simple example, but I just want to demonstrate the logic behind the proof that I am questioning) Now the correct response would be to start with the...- cerealkiller
- Thread
- Counterexample Inequality Proof
- Replies: 6
- Forum: General Math
-
M
MHB Definite Integration of a concave upward function- Inequality
- mathisfun1
- Thread
- Concave Function Inequality Integration
- Replies: 11
- Forum: Calculus
-
D
How to Prove a Complex Inequality with Complex Algebra
Homework Statement Let b and a be two complex numbers. Prove that |1+ab| + |a + b| ≥ √(|a²-1||b²-1|). Homework Equations Complex algebra The Attempt at a Solution I don't know how to proceed. I posted it here to get some ideas :p- Dinheiro
- Thread
- Complex Inequality
- Replies: 1
- Forum: Precalculus Mathematics Homework Help
-

MHB Proving Inequality: $a^{2a}b^{2b}c^{2c} > a^{b+c}b^{c+a}c^{a+b}$
given:$a>b>c>0$ prove:$a^{2a}b^{2b}c^{2c}>a^{b+c}b^{c+a}c^{a+b}$- Albert1
- Thread
- Challenge Inequality
- Replies: 2
- Forum: General Math
-

MHB Can you prove the inequality challenge?
Let $x\ge \dfrac{1}{2}$ be a real number and $n$ a positive integer. Prove that $x^{2n}\ge (x-1)^{2n}+(2x-1)^n$.- anemone
- Thread
- Challenge Inequality
- Replies: 2
- Forum: General Math
-

Graduate What is the Schwarz Inequality and Its Applications?
[SIZE="4"]Definition/Summary the Schwarz inequality (also called Cauchy–Schwarz inequality and Cauchy inequality) has many applications in mathematics and physics. For vectors a,b in an inner product space over \mathbb C: \|a\|\|b\| \geq |(a,b)| For two complex numbers a,b ...- Greg Bernhardt
- Thread
- Inequality
- Replies: 1
- Forum: Topology and Analysis
-

Undergrad What is the AM-GM-HM Inequality and How is it Useful?
[SIZE="4"]Definition/Summary Arithmetic-Geometric-Harmonic Means Inequality is a relationship between the size of the arithmetic mean (AM), geometric mean (GM) and harmonic mean (HM) of a given set of positive real numbers. It is often very useful in analysis. [SIZE="4"]Equations {\rm...- Greg Bernhardt
- Thread
- Inequality
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-
W
Proof for the greatest integer function inequality
Can anyone help me prove the greatest integer function inequality- n≤ x <n+1 for some x belongs to R and n is a unique integer this is how I tried to prove it- consider a set S of Real numbers which is bounded below say min(S)=inf(S)=n so n≤x by the property x<inf(S) + h we have...- wellorderingp
- Thread
- Function Inequality Integer Proof
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-

MHB Is the Inequality of Series Proven with 1 to 99 and 2 to 100?
prove : $\dfrac {1\times 3 \times 5\times------\times 99}{2\times 4\times 6\times --\times {100}}>\dfrac {1}{10\sqrt 2}$- Albert1
- Thread
- Inequality
- Replies: 2
- Forum: General Math
-

MHB Prove Inequality: $18<\sum\limits_{i=2}^{99}\dfrac 1{\sqrt i} <19$
prove : $18<1+\dfrac {1}{\sqrt 2}+\dfrac {1}{\sqrt 3}+----+\dfrac{1}{\sqrt {99}}<19$- Albert1
- Thread
- Inequality
- Replies: 2
- Forum: General Math
-

MHB How can I show the inequality?
Hey! (Mmm) I have to define an asymptotic upper and lower bound of the recursive relation $T(n)=3 T(\frac{n}{3}+5)+\frac{n}{2}$. Firstly,I solved the recursive relation: $T'(n)=3 T'(\frac{n}{3})+\frac{n}{2}$,using the master theorem: $$a=3 \leq 1, b=3>1, f(n)=\frac{n}{2} \text{ asymptotically...- evinda
- Thread
- Inequality
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-
M
Proof of Inequality Between Lower and Upper Bounds
Convergence of Divergent Series Whose Sequence Has a Limit Homework Statement Suppose ∑a_{n} is a series with lim a_{n} = L ≠ 0. Obviously this diverges since L ≠ 0. Suppose we make the new series, ∑(a_{n} - L). My question is this: is there some sufficient condition we could put solely...- muzak
- Thread
- Bounds Inequality Proof
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
R
MHB Proving an inequality with square roots
This is problem 13 from section I 4.7 of Apostol's Calculus Volume 1: Prove that $$2(\sqrt{n+1}-\sqrt{n})<\frac{1}{\sqrt{n}}<2(\sqrt{n}-\sqrt{n-1})$$ if $$n\geq 1$$. Then use this to prove that $$2\sqrt{m}-2<\displaystyle\sum_{n=1}^m\frac{1}{\sqrt{n}}<2\sqrt{m}-1$$ if $$m\geq 2$$. I have... -

MHB Can Inequalities Be Proven? A Solution to a Complex Equation
Prove that $\sqrt{x^4+7x^3+x^2+7x}+3\sqrt{3x}\ge10x-x^2$.- anemone
- Thread
- Challenge Inequality
- Replies: 2
- Forum: General Math
-
N
Graduate "Violation of Bell's inequality in fluid mechanics"
I thought it might be interesting to point out this article: Title: Violation of Bell's inequality in fluid mechanics Authors: Robert Brady and Ross Anderson (Cambridge) Abstract:- nonequilibrium
- Thread
- Fluid Fluid mechanics Inequality Mechanics
- Replies: 7
- Forum: Quantum Physics
-
K
MHB Finding conditions for which an inequality holds
Hello, I do not know if this is the right place to post this question, but I believe it falls under algebra. Please redirect me if appropriate. Question: How can I show that $$P-QR^3<\frac{R^4}{C}$$ for $$C,P,Q,R > 0?$$ Thanks.- kalish1
- Thread
- Conditions Inequality
- Replies: 1
- Forum: General Math
-

MHB Challenging Trigonometric Inequality: Can You Prove It?
$0<\alpha, \beta<\dfrac {\pi}{2}$ prove :$\dfrac {1}{cos^2\alpha}+\dfrac {1}{sin^2\alpha\,sin^2\beta\, cos^2\beta}\geq 9$ and corresponding $\alpha$, and $\beta$- Albert1
- Thread
- Inequality Trigonometric
- Replies: 5
- Forum: General Math
-

MHB Can You Prove $6^{33}>3^{33}+4^{33}+5^{33}?
Prove that $6^{33}>3^{33}+4^{33}+5^{33}$.- anemone
- Thread
- Challenge Inequality
- Replies: 3
- Forum: General Math
-
I
Dirac notation Schwarz Inequality Proof
Homework Statement This isn't really a problem so much as me not being able to see how a proof has proceeded. I've only just today learned about Dirac notation so I'm not too good at actually working with it. The proof in the book is: |Z> = |V> - <W|V>/|W|^2|W> <Z|Z> = <V - ( <W|V>/|W|^2 ) W|...- interdinghy
- Thread
- Dirac Dirac notation Inequality Notation Proof
- Replies: 6
- Forum: Introductory Physics Homework Help
-

MHB Is There a Solution to the Challenge of Inequality?
Given that $0<k,\,l,\,m,\,n<1$ and $klmn=(1-k)(1-l)(1-m)(1-n)$, show that $(k+l+m+n)-(k+m)(l+n)\ge1$.- anemone
- Thread
- Challenge Inequality
- Replies: 2
- Forum: General Math
-

MHB Find Minimum of Inequality Expression: 0<x<π/2
I am trying to find the minimum of the following expression: $$\frac{\sin^2x+8\cos^2x+8\cos x+\sin x}{\sin x\cos x}\,\,\,,0<x<\frac{\pi}{2}$$ I know I can bash this with calculus but the expression has a nice minimum value (=17) which makes me think that it can be solved by use of some... -
Graduate Did I Mess Up My CHSH Inequality Simulation?
I never heard of the CSHS Inequality until I read it in another thread. The other interesting item was this: I think an important part of that discussion is the more hits are ignored, the easier it is for local realistic theories to score over 2.00. So I just had to try. For those familiar...- .Scott
- Thread
- Inequality Noise
- Replies: 1
- Forum: Quantum Physics
-
M
Matrices and rank inequality exercise
The problem statement Let ##A ∈ K^{m×n}## and ##B ∈ K^{n×r}## Prove that min##\{rg(A),rg(B)\}≥rg(AB)≥rg(A)+rg(B)−n## My attempt at a solution (1) ##AB=(AB_1|...|AB_j|...|AB_r)## (##B_j## is the ##j-th## column of ##B##), I don't know if the following statement is correct: the columns of...- mahler1
- Thread
- Exercise Inequality Matrices rank
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-

MHB What are the real values of $k$ that satisfy the trigonometric inequality?
Find all real $k$ such that $0<k<\pi$ and $\dfrac{8}{3\sin k-\sin 3k}+3\sin^2 k\le 5$.- anemone
- Thread
- Inequality Trigonometric
- Replies: 1
- Forum: General Math
-

MHB Can You Prove Inequality Challenge II?
The cubic polynomial $x^3+mx^2+nx+k=0$ has three distinct real roots but the other polynomial $(x^2+x+2014)^3+m(x^2+x+2014)^2+n(x^2+x+2014)+k=0$ has no real roots. Show that $k+2014n+2014^2m+2014^3>\dfrac{1}{64}$.- anemone
- Thread
- Challenge Inequality
- Replies: 2
- Forum: General Math
-

MHB Inequality Challenge: Prove $b^3+a^3 \le 2$
The positive real $a$ and $b$ satisfy $b^3+a^2\ge b^4+a^3$. Prove that $b^3+a^3\le 2$.- anemone
- Thread
- Challenge Inequality
- Replies: 2
- Forum: General Math
-

MHB Why Does the Inequality Hold in This Taylor Series Expansion?
Hello! (Wasntme) I want to find the Taylor series of the function $f(x)=\log(1+x), x \in (-1,+\infty)$. We take $\xi=0, I=(-1,1)$ It is: $$f'(x)=(1+x)^{-1}, f''(x)=-1 \cdot (1+x)^{-2}, f'''(x)=2 \cdot (1+x)^{-3} , f^{(4)}(x)=-6 \cdot (1+x)^{-4}, f^{(5)}(x)=24(1+x)^{-5}$$ So,we see that...- evinda
- Thread
- Inequality
- Replies: 9
- Forum: Topology and Analysis
-
B
MHB Maximum volume using AM GM inequality
Hi everyone, I'm a bit confused with this question. An airline demands that all carry-on bags must have length + width + height at most 90cm. What is the maximum volume of a carry-on bag? How do you know this is the maximum? [Note: You can assume that the airline technically mean "all carry...- batch3
- Thread
- gm Inequality Maximum Volume
- Replies: 4
- Forum: General Math
-
D
MHB Prove AM-GM Inequality: What Values to Use?
Could someone please help me with this question: What values are we meant to use to prove this inequality? many thanks- delc1
- Thread
- gm Inequality
- Replies: 3
- Forum: Set Theory, Logic, Probability, Statistics
-

MHB Proving an Inequality: $(\sin\, x)^{\sin\, x}\,<(\cos\, x)^{\cos\, x}$
One of the 2 inequalities $(\sin\, x)^{\sin\, x}\,<(\cos\, x)^{\cos\, x} $ and $(\sin\, x)^{\sin\, x}\,>(\cos\, x)^{\cos\, x} $ is always true for all x such that $0 \,< \, x \, < \pi/4$ Identify the inequality and prove it- kaliprasad
- Thread
- Inequality
- Replies: 1
- Forum: General Math
-

MHB Can You Prove the Inequality Challenge VI for Arctan Sequences?
If $\alpha_n=\arctan n$, prove that $\alpha_{n+1}-\alpha_n<\dfrac{1}{n^2+n}$ for $n=1,\,2,\,\cdots$. -

MHB Inequality Challenge V: Prove $(a+b)^{a+b} \le (2a)^a(2b)^b$
Prove that for any real numbers $a$ and $b$ in $(0,\,1)$, that $(a+b)^{a+b}\le (2a)^a(2b)^b$.- anemone
- Thread
- Challenge Inequality
- Replies: 3
- Forum: General Math
-
D
High School Is the Inequality with Absolute Values |x+y| ≤ |x| + |y| True?
Wonder if this is true or just mistype: |x+y| \leq |x| +|y| If this is true how to proof because cannot find it out anywhere written Regards- DrunkenPhD
- Thread
- Absolute Absolute values Inequality
- Replies: 4
- Forum: Calculus
-
Q
Graduate Can Complex Numbers be Compared Using Greater-Than and Less-Than Relations?
Are the less than (<) and greater than(>) relations applicable among complex numbers? By complex numbers I don't mean their modulus, I mean just the raw complex numbers.- quawa99
- Thread
- Complex Complex numbers Inequality Numbers
- Replies: 1
- Forum: Topology and Analysis