Theorem Definition and 1000 Threads
-

Use Remainder theorem to find factors of ##(a-b)^3+(b-c)^3+(c-a)^3##
My first approach; ##(a-b)^3+(b-c)^3+(c-a)^3=a^3-3a^2b+3ab^2-b^3+b^3-3b^2c+3bc^2-c^3+c^3-3c^2a+3ca^2-a^3## ##=-3a^2b+3ab^2-3b^2c+3bc^2-3c^2a+3ca^2## what i did next was to add and subtract ##3abc## ...just by checking the terms ( I did not use...- chwala
- Thread
- Factors Remainder Remainder theorem Theorem
- Replies: 4
- Forum: Precalculus Mathematics Homework Help
-

Undergrad The second uniqueness theorem in electrostatics
Does the second uniqueness theorem just say that if there is an electric field that satisfies Gauss's law for a surface surrounding each conductor + a surface enclosing all the conductors, it is indeed the true electric field, and no other electric field will satisfy those conditions?- Ahmed1029
- Thread
- Conductors Electrostatics Theorem Uniqueness Uniqueness theorem
- Replies: 5
- Forum: Electromagnetism
-

Undergrad A question about the Second Uniqueness Theorem in electrostatics
in this example in Griffiths' electrodynamics, he says the following :(Figure 3.7 shows a simple electrostatic configuration, consisting of four conductors with charges ±Q, situated so that the plusses are near the minuses. It all looks very comfort- able. Now, what happens if we join them in...- Ahmed1029
- Thread
- Conductors Electrostatics Theorem Uniqueness Uniqueness theorem
- Replies: 11
- Forum: Electromagnetism
-

Graduate Prime Number Powers of Integers and Fermat's Last Theorem
From my research I have found that since Fermat proved his last theorem for the n=4 case, one only needs to prove his theorem for the case where n=odd prime where c^n = a^n + b^n. But I am not clear on some points relating to this. For example, what if we have the term (c^x)^p, where c is an...- e2m2a
- Thread
- Integers Prime Theorem
- Replies: 1
- Forum: General Math
-

High School Mean-Value Theorem, Taylor's formula, and error estimation
Hi, PF Taylor's formula provides a formula for the error in a Taylor approximation ##f(x)\approx{P_{n}(x)}## similar to that provided for linear approximation. Observe that the case ##n=0## of Taylor's formula, namely, ##f(x)=P_{0}(x)+E_{0}(x)=f(a)+\dfrac{f'(s)}{1!}(x-a)##, is just the...- mcastillo356
- Thread
- Error Estimation Formula Theorem
- Replies: 3
- Forum: Calculus
-

Graduate Confused by a theorem in Milnor-Stasheff
The k-th Pontrjagin class of a real vector bundle is defined as the 2k-Chern class of the complexified bundle. Therefor, a Pontrjagin class lives in cohomology with integer coefficients. But then the statement of Theorem 15.9 is that if the coefficient ring is taken to be a PID \Lambda...- quasar987
- Thread
- Confused Theorem
- Replies: 4
- Forum: Topology and Analysis
-

Engineering Question about a circuit to be solved with Norton's theorem
Hello guys, I am new here. I was wondering whether I could get some help about the highlighted part. What I don't understand is why we are able to ignore the 5-ohms resistor when we have short circuited terminals a-b. Thanks in advance.- link223
- Thread
- Circuit Theorem
- Replies: 2
- Forum: Engineering and Comp Sci Homework Help
-
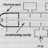
Undergrad Intermediate Axis Theorem.... fun to learn it again with You Tube
A friend of mine shared a YouTube video with me, saying he was sure I would love it. He described it as very strange with a rotating wingnut in the space station flipping over on its rotation axis, over and over, while it spun rapidly. After watching the video, I verified I was taught the...- CPW
- Thread
- Axis Fun Theorem Tube
- Replies: 3
- Forum: Other Physics Topics
-
B
Undergrad Does Axler's Spectral Theorem Imply Normal Matrices?
Going through Axler's awful book on linear algebra. The complex spectral theorem (for operator T on vector space V) states that the following are equivalent: 1) T is normal 2) V has an orthonormal basis consisting of eigenvectors of T and 3) the matrix representation of T is diagonal with...- boo
- Thread
- Matrices Normal Theorem
- Replies: 3
- Forum: Linear and Abstract Algebra
-

Finding the Wrong Answer with Stokes' Theorem
From Stokes' theorem: ##\int_{C}^{}\vec F\cdot d\vec r=\iint_{S}^{}curl\vec F\cdot d\vec S=\iint_{D}^{}curl\vec F\cdot(\vec r_u \times \vec r_v)dA ## To get to the latter surface integral, I started by parametrizing the triangular surface in ##uv## coordinates as: $$\vec r=<1-u-v,u,v>, 0\leq...- greg_rack
- Thread
- Stokes Theorem
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-

Calculating the Line Integral of F over C: Stokes' Theorem and Symmetry
From Stokes we know that ##\iint_{\textbf{S}}^{}curl \textbf{F}\cdot d\textbf{S}=\int_{C}^{}\textbf{F}\cdot d\textbf{r}##. Now, we can calculate the surface integral of the curl of F by calculating the line integral of F over the curve C. The latter ends up being 0(I calculated it parametrizing...- greg_rack
- Thread
- Integral Line Line integral Stokes Symmetry Theorem
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-
O
Undergrad Equipartition theorem and Drag
If I have a many-body Hamiltonian, and I choose a coordinate x with canonical momentum p, I can say that by the generalized equipartition theorem that <p(dH/dx)> = -<p(dp/dt)> = 0 Since p and x are distinct phase space variables, and since by the Hamiltonian equations of motion the force...- Opus_723
- Thread
- Drag Theorem
- Replies: 2
- Forum: Thermodynamics
-
H
Kinematic Problem w/ Parabola: Solving w/ KE Theorem?
This is not really a homework problem (it could be made to be though). I kind of made it up, inspired by a youtube math challenge problem involving parabolas, a water fountain where A = 1, R = 3, and H = 3. The solution given (h = 9/4) was based off simple math utilizing vertex form of a...- h1a8
- Thread
- Kinematic Parabola Theorem
- Replies: 25
- Forum: Introductory Physics Homework Help
-
C
Undergrad Where to find this uniqueness theorem of electrostatics?
There is a nice uniqueness theorem of electrostatics, which I have found only after googling hours, and deep inside some academic site, in the lecture notes of Dr Vadim Kaplunovsky: Notice that the important thing here is that only the NET charges on the conductors are specified, not their...- coquelicot
- Thread
- Electro static Electrostatic Electrostatic charges Electrostatics Laplace equation Poisson equation Theorem Uniqueness Uniqueness theorem
- Replies: 27
- Forum: Electromagnetism
-
L
[Bayes' Theorem] Finding the probability of guessing correctly
I calculated the probability of box 1/2/3 given white. P(Box 1 | white) = P(Box 1)*P(White | Box 1)/(P(Box 1)*P(White | Box 1) + P(Not Box 1)*P(White | Not Box 1)) = ((1/3)*(1/2)) / (((1/3)*(1/2) + (2/3)*(5/7) = 7/27 P(Box 2 | white) = P(Box 2)*P(White | Box 2)/(P(Box 2)*P(White | Box 2) +...- LokLe
- Thread
- Probability Theorem
- Replies: 13
- Forum: Calculus and Beyond Homework Help
-

Graduate Interpretations of the No Communication Theorem
Moderator's note: Spin-off from previous thread due to topic change. Not in the sense in which it is used in the no communication theorem. That sense is basically the information theoretic sense, which in no way requires humans to process or even be aware of the information.- PeterDonis
- Thread
- Communication Interpretations Theorem
- Replies: 47
- Forum: Quantum Interpretations and Foundations
-

Understanding the Mean value theorem
Can we have two tangents (two turning points) within the given two end points just asking? I know the theorem holds when there is a tangent to a point ##c## and a secant line joining the two end points. Or Theorem only holds for one tangent point. Cheers- chwala
- Thread
- Mean Mean value theorem Theorem Value
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-

Green's reciprocity theorem about current density and magnetic field
I have to prove three equations above. For first two equations, I've been thought and made reasonable answer by using a definition of the electricfield. However, for third, I can't use a definition of a magnetic field due to the cross product Like J_2 X J_1 X (r_2 - r_1). I think three of 'em...- SanaiBongchul
- Thread
- Current Current density Density Elecrtomagnetism Field Magnetic Magnetic field Precipitation Theorem
- Replies: 1
- Forum: Advanced Physics Homework Help
-
E
Graduate The Factorization Theorem in Particle Physics
I have been tasked with calculating amplitudes of a B meson decaying to a photon and lepton/lepton anti-neutrino pair ,upto one loop and have pretty much never seen this thing before. I will ask my questions along the way as I describe what I am doing. This factorization theorem seems to go thus...- Elmo
- Thread
- Factorization Particle Particle physics Physics Theorem
- Replies: 6
- Forum: High Energy, Nuclear, Particle Physics
-
H
Undergrad How is uniqueness about the determinant proved by this theorem?
Let me first list the four axioms that a determinant function follows: 1. ## d (A_1, \cdots, t_kA_k, \cdots, A_n)=t_kd(A_1, \cdots A_k, \cdots, A_n)## for any ##A_k## and ##t_k## 2. ##d(A_1, \cdots A_k + C , \cdots A_n)= d(A_1, \cdots A_k, \cdots A_n) + d(A_1, \cdots C, \cdots A_n)## for any...- Hall
- Thread
- Determinant Determinants Linear algebra Theorem Uniqueness
- Replies: 10
- Forum: Linear and Abstract Algebra
-

High School Work energy theorem by variable force
Its Good to be Back! From Resnik, Fundamentals of physics: Consider a particle of mass m, moving along an x-axis and acted on by a net force F(x) that is directed along that axis. The work done on the particle by this force as the particle moves from position ##x_i## to position ##x_f## is given...- rudransh verma
- Thread
- Classical mechanics Energy Force Theorem Variable Variable force Work Work energy Work energy theorem
- Replies: 23
- Forum: Mechanics
-
P
Undergrad Mean value theorem - prove inequality
I don't need an answer (although I don't have sadly, it's from a test). I need just a tip on how to start it... i cannot use Taylor in here (##\ln(x)## is not Taylor function), therefore, its only MVT, but I don't know which point I should try... since I must get the annoying ##\ln(x)##...- physics1000
- Thread
- Inequality Mean Mean value theorem Theorem Value
- Replies: 19
- Forum: Calculus
-

MHB Checking Proof of Theorem 6.2.8 Part (ii)
I have completed a formal proof of D&K Theorem 6.2.8 Part (ii) ... but I am unsure of whether the proof is correct ... so I would be most grateful if someone could check the proof and point out any errors or shortcomings ... Theorem 6.2.8 reads as follows: Attempted Proof of Theorem 6.2.8...- Math Amateur
- Thread
- Proof Theorem
- Replies: 2
- Forum: Topology and Analysis
-

MHB How can we prove the inequality for the supremum and infimum of f*g and f*g?
I am reading J. J. Duistermaat and J. A. C. Kolk: Multidimensional Analysis Vol.II Chapter 6: Integration ... I need help with the proof of Theorem 6.2.8 Part (iii) ...The Definition of Riemann integrable functions with compact support and Theorem 6.2.8 and a brief indication of its proof...- Math Amateur
- Thread
- Compact Functions Proof Properties Riemann Support Theorem
- Replies: 2
- Forum: Topology and Analysis
-
A
Green's theorem with a scalar function
Greetings! My question is: is it possible to use the green theorem to compute the circulation while in presence of a scalar function ? I know how to solve by parametrising each part but just in case we can go faster? thank you!- Amaelle
- Thread
- Function Green's theorem Scalar Theorem
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
T
Graduate Noether's theorem time invariance -- mean value theorem use?
how does the first step use mean value theorem? I don't get it , can anyone explain , thanks. -

Use binomial theorem to find the complex number
This is also pretty easy, ##z^5=(a+bi)^5## ##(a+bi)^5= a^5+\dfrac {5a^4bi}{1!}+\dfrac {20a^3(bi)^2}{2!}+\dfrac {60a^2(bi)^3}{3!}+\dfrac {120a(bi)^4}{4!}+\dfrac {120(bi)^5}{5!}## ##(a+bi)^5=a^5+5a^4bi-10a^3b^2-10a^2b^3i+5ab^4+b^5i## ##\bigl(\Re (z))=a^5-10a^3b^2+5ab^4## ##\bigl(\Im (z))=...- chwala
- Thread
- Binomial Binomial theorem Complex Complex number Theorem
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
N
Undergrad Frontiers in Physics had 2 papers quest. Bell's theorem, any othrs?
One is fr. worker at U. Karlsruhe, another fr. Israeli res. The latter argued findings can be integrated into classical physics.- ndvcxk123
- Thread
- Bell's theorem Papers Physics Theorem
- Replies: 2
- Forum: Quantum Physics
-

Solve the equation involving binomial theorem
$$(7-6x)^3+(7+6x)^3=1736$$ $$⇒(7^3(1-\frac {6}{7}x)^3+(7^3(1+\frac {6}{7}x)^3=1736$$ $$343[1-\frac {18}{7}x+\frac {216}{98}x^2-\frac{1296}{2058}x^3]+343[1+\frac {18}{7}x+\frac {216}{98}x^2+\frac{1296}{2058}x^3]=1736$$ $$343[2+\frac {432}{98}x^2]=1736$$ $$686+\frac {148,176}{98}x^2=1736$$ $$\frac...- chwala
- Thread
- Binomial Binomial theorem Theorem
- Replies: 16
- Forum: Calculus and Beyond Homework Help
-
M
Graduate Dynamic Systems: Poincaré-Bendixson Theorem finite # of equilibria
Homework Statement:: Can someone explain the finite number of equilibria outcome of the Poincaré-Bendixson Theorem? Relevant Equations:: Poincaré-Bendixson Theorem [Mentor Note -- General question moved from the schoolwork forums to the technical math forums] Hi, I was reading notes in...- Master1022
- Thread
- Dynamic dynamic systems Dynamical systems Equilibria Finite Systems Theorem
- Replies: 4
- Forum: Differential Equations
-
S
Undergrad Is this statement an aspect of the Hairy Ball or Fixed Point Theorem?
“Given any class of mutually exclusive classes, of which none is null, there is at least one class which has exactly one term in common with each of the given classes…” The reason this statement sounds like one of those theora is that I recall reading a Time-Life book on Mathematics, and there...- swampwiz
- Thread
- Ball Fixed point Point Theorem
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-
D
Undergrad Liouville's Theorem and Poincare Recurrence Theorem
Hi. I am working through some notes on the above 2 theorems. Liouville's Theorem states that the volume of a region of phase space is constant along Hamiltonian flows so i assume this means dV/dt = 0 In the notes on the Poincare Recurrence Theorem it states that if V(t) is the volume of phase... -

Virial Theorem for an expanding globular cluster
I attached a file which shows my attempt to resolve this problem with the possible two pair interaction which gives us the kinetic energy of the cluster in an expanding system, at least I think so. But to be honest I´m more or less completely stuck with this question and I would be glad if...- Barbequeman
- Thread
- globular Globular cluster Theorem Virial theorem
- Replies: 3
- Forum: Introductory Physics Homework Help
-

High School Question in the momemtum-impulse theorem derivation
when the net force is constant then Q1. rate of change of momentum (dp/dt) is zero or constant Q2. assuming dp/dt is constant we replaced it with ----> p2-p1(total change in momentum ) ? how?- just NOTHING
- Thread
- Derivation Impulse momentum Theorem
- Replies: 9
- Forum: Mechanics
-

High School I want this short proof of the Bolzano-Weierstrass Theorem checked please
Let ##X## be a bounded subset of ##\mathbb{R}## with infinite cardinality. We consider a countably-infinite subset of ##X##. We write this set as a sequence to be denoted ##\{a_n\}_{n\in\mathbb{N}}##. Now define ##A## to be the set of points in the sequence with the property that for each...- Eclair_de_XII
- Thread
- Proof Short Theorem
- Replies: 8
- Forum: Calculus
-

High School Proving half of the Heine-Borel theorem
Let ##X## be a closed and bounded subset of the real numbers. Let ##\{x_i\}_{i\in I}##, for some index ##I##, represent the set of limit points of ##X##. Since ##X## is closed, it must follow that ##\{x_i\}_{i\in I}\subset X##. Hence, the set of limit points must be bounded. Let ##\{U_j\}_{j\in...- Eclair_de_XII
- Thread
- Theorem
- Replies: 3
- Forum: Calculus
-
R
I have a real simple question about the Pythagoras theorem
Here is the link. https://www.grc.nasa.gov/www/BGH/sincos.html Sorry just a little rusty on Pythagoras theorem. I mean the formula still holds but in order to find the opposite and the adjacent the opposite becomes the adjacent and vice versa .- rgtr
- Thread
- Pythagoras Theorem
- Replies: 5
- Forum: Precalculus Mathematics Homework Help
-
A
Engineering Is my method of solving this correct? Superposition theorem
Hello! Consider this circuit Now I want to calculate the current Ik. The values are given as follows; Uq1 = 12 V Uq2 = 18V R1 = R2 = 8 Ohm R3 = R4 = 20 Ohm My approach was using the Superposition theorem. First I deactived Uq2 and left Uq1 active. Now if I am not mistaken the resistors R2 R3...- arhzz
- Thread
- Method Superposition Superposition theorem Theorem
- Replies: 15
- Forum: Engineering and Comp Sci Homework Help
-

Undergrad Darboux theorem for symplectic manifold
Hi, I am missing the point about the application of Darboux theorem to symplectic manifold case as explained here Darboux Theorem. We start from a symplectic manifold of even dimension ##n=2m## with a symplectic differential 2-form ##w## defined on it. Since by definition the symplectic 2-form...- cianfa72
- Thread
- Differential calculus Differential forms Differential geometry Manifold Symplectic Symplectic geometry Theorem
- Replies: 4
- Forum: Differential Geometry
-
K
Graduate Uncertainties on Bayes' theorem
Hello! I have a setup consisting of some charged particles each of which is produced at a different position, ##(x_i,y_i,z_i)##. I don't know the exact position, but I know that each of the 3 variables is normally distributed with mean zero and standard deviation of 3 mm. What I measure in the...- kelly0303
- Thread
- Theorem Uncertainties
- Replies: 19
- Forum: Set Theory, Logic, Probability, Statistics
-

Undergrad [Congruence class] Proof of modular arithmetic theorem
Could someone explain why ##[a][x_0]=[c]\iff ax_0\equiv c\, (mod\, m)##? My instructor said it came from the definition of congruence class. But I am not convinced.- Leo Liu
- Thread
- Arithmetic Class Proof Theorem
- Replies: 2
- Forum: Set Theory, Logic, Probability, Statistics
-
M
Graduate Energy, mass and Noether’s theorem
Mentors note: split from https://www.physicsforums.com/threads/energy-mass-equivalence.1003564/ How do you measure energy?- md2perpe
- Thread
- Energy Mass Theorem
- Replies: 74
- Forum: Special and General Relativity
-
D
Use Liouville's theorem to show that two functions are equal
##lim_{|z|\rightarrow \infty}\frac{f}{g}=1\neq \frac{\infty}{\infty}## so ##lim_{|z|\rightarrow \infty}f\neq \infty## and ##lim_{|z|\rightarrow \infty}g\neq \infty##. Because f(z) and g(z) are bounded and entire, f(z) and g(z) are constant functions by Liouville's theorem . f(z) and g(z) are...- docnet
- Thread
- Functions Theorem
- Replies: 10
- Forum: Calculus and Beyond Homework Help
-

Impulse-momentum theorem problem
The solution is from ##fdt=d(mv)=mdv+vdm## and separate the variables and then integrate them. But at first I tried this method. At time ##t##, suppose the mass of the cart is ##m##, and its velocity is ##v##. And suppose at time ##t+dt##, its mass will be ##m-\rho dt##, and its velocity...- Haorong Wu
- Thread
- Theorem
- Replies: 14
- Forum: Introductory Physics Homework Help
-

Python Python’s Sympy Module and the Cayley-Hamilton Theorem
Continue reading...- Mark44
- Thread
- module Theorem
- Replies: 1
- Forum: Programming and Computer Science
-
K
Graduate Matrix proof of Euler's theorem of rotation
The question arises the way Goldstein proves Euler theorem (3rd Ed pg 150-156 ) which says: " In three-dimensional space, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point"... -
F
Graduate To understand the Darboux theorem
Darboux theorem says a derivative function must have an intermediate value theorem without requiring the derivative function to be continuous. Why is this property not true for any continuous function in its intermediate value theorem? -
K
Graduate Hooke's law, Bertrand's theorem and closed orbits
Bertrand's Theorem says : the only forces whose bounded orbits imply closed orbits are the Hooke's law and the attractive inverse square force. I'm looking at the hookes law ##f=-k r## and try to see explicitly that the orbit is indeed closed. I use the orbit equation ##\frac{d^{2} u}{d... -
Z
Possible to use work-energy theorem from a non-inertial frame?
In learning about translational and rotational motion, I solved a problem involving a wheel rolling down an inclined plane without slipping. There are multiple ways to solve this problem, but I want to focus on solutions using energy. Now to my questions. The reference frame in the posted...- zenterix
- Thread
- Frame Newtonian mechanics Non-inertial frame Rotational mechanics Theorem Work-energy Work-energy theorem
- Replies: 1
- Forum: Introductory Physics Homework Help
-

Undergrad Stokes' theorem and surface integrals
Hi, So my goal is to compute the integral of the "curl" of the vector field ##A_i(x_i)## over a 2-dimensional surface. Following a physics book that I am reading, I introduce the antisymmetric 2-nd rank tensor ##\Omega_{ij}##, defined as: $$\Omega_{ij} = \frac {\partial A_i}{\partial x_j} -...