adarpodracir
- 5
- 0
Hi there,
I have a question regarding this statement:
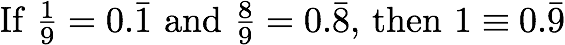
My question is whether we can say so...
Thank you very much!
I have a question regarding this statement:
My question is whether we can say so...
Thank you very much!