karush
Gold Member
MHB
- 3,240
- 5
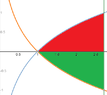
Draw the regions of integration and write the following integrals as a single iterated integral.
$$\displaystyle\int_{0}^{1} \int_{e^y}^{e} f(x,y)\,dx\,dy + \int_{-1}^{0} \int_{e^{-y}}^{e}f(x,y) \,dx\,dy$$
ok haven't done this before so kinda clueless
$$\displaystyle\int_{0}^{1} \int_{e^y}^{e} f(x,y)\,dx\,dy + \int_{-1}^{0} \int_{e^{-y}}^{e}f(x,y) \,dx\,dy$$
ok haven't done this before so kinda clueless