2 DOF oscillator max force reponse

[saxymon]

(NOTE, this is not a homework problem, but it sure seems like one)

Hello,

I am mounting a component onto structure and I need to determine the maximum force input into the component.

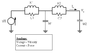
My system can be represented by a base driven two degree of freedom oscillator:

http://www.freeimagehosting.net/newuploads/xowmr.png

I need to determine the force applied to m2:

F = k2*(x2-x1) + c2*(x2-x1)

This force needs to be a function of (m1,m2,c1,c2,k1,k2,y) and not of (x1,x2).
Basically, for a given input y, what will the be force response on m2.

Every time I solve the system of equations, my result is a function of x1 and/or x2.


Thank you in advance for your help!

p.s. If it is easier, feel free to remove the dampers from the system. An un-damped system will work for my purposes.

 

[saxymon]

As for an attempt at the solution:

my matrix system of equations is...

[m1 0 ; 0 m2] [x''1 ; x''2] + [k1+k2 -k2 ; -k2 k2] [x1 ; x2] = [0 ; k1] [0 y]

Interestingly enough, the force I need to recover is naturally in the lower portion of the equation giving:

F = k1*y - m2*x''2

I make the reduction to

F = k1*y + Wn^2*m2*x2

but still was not able to remove all of the x2's and x1's (after making a number of substitutions).

 

[rude man]

You have two equations and two unknowns (x₁ and x₂). You can solve for them as functions of m1,m2,c1,c2,k1,k2, and y.

(I would use the Laplace transform, but there is of course a time-domain way to solve them also. I don't have that info on hand.

 

[gneill]

Your mechanical system can be modeled as an electrical circuit (an "analog" system). Use a simulator (Spice) to characterize the maximal force versus various "input signals".

Assuming that voltage represents velocity and current represents force, the mechanical elements have particular electrical analogs:

Spring = Inductor
Damper = Resistor
Mass = Capacitor
Force = Current
Velocity = Voltage

Force inputs become current sources. Initial velocities (of masses) become initial voltages on capacitors. Velocity inputs are okay -- they become voltage inputs, so if you want to determine how your system responds to a given motion driving it, characterize the motion in terms of its velocity.

In the above circuit I_o represents the force that's applied to the mass M2.