2-Resistor, 2-Capacitor Circuit with Switch

[Mark Zhu]

Homework Statement

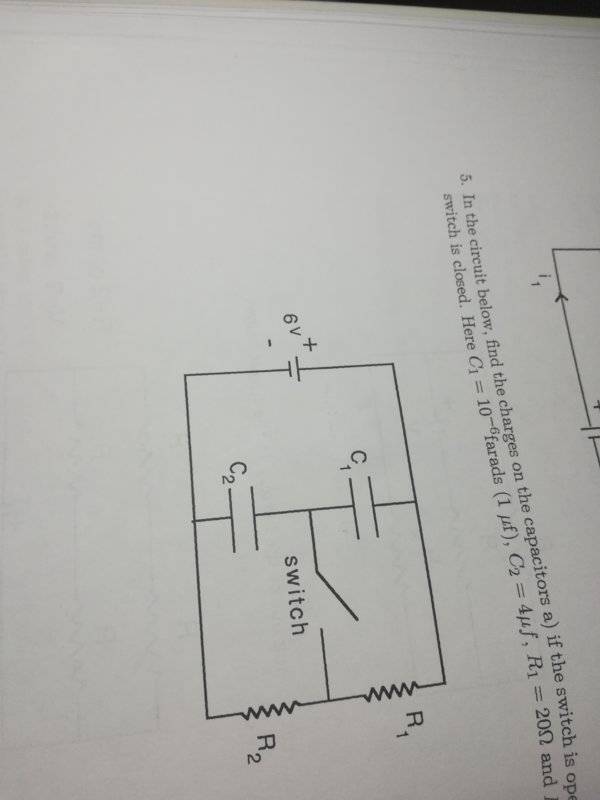
In the circuit below, find the charges on the capacitors a) if the switch is open, b) if the switch is closed. Here C1 = 1 microfarads, C2 = 4 microfarads, R1 = 20 ohms and R2 = 40 ohms.

Relevant Equations

V = iR
Q = CV

I already did part a and got the correct answer of 4.8 microC. However, I am unsure how to approach part b, where the switch is closed and apparently the two capacitors end up with different charges. For part b, since there is a path between the two capacitors, I don't know if I am able to combine the two capacitors into an equivalent capacitor. According to the textbook, the solution is that Q1 is 2 microC and Q2 is 16 microC. Any help is appreciated.

 

[BvU]

Hi,

Well, what do you get for the voltage over C1 if you apply your first relevant equation ?

(after you determined -- qualitatively -- what happens with the current through the switch when it is closed and afterwards )

 

[Mark Zhu]

I think I got it, thank you.

 

[BvU]

With the answers given it's a piece of cake