2D momentum piece breaks problem

[coldsteel]

1.A piece of ice falls on a frozen lake and breaks up into three pieces which go off in the directions shown in the diagram below. The mass of the bigger piece is 4 kg and it moves with a speed of 4 m/s straight down, If the two smaller pieces are 2 kg each and break off at 45 degrees each. What would be their speed right after the breakup?

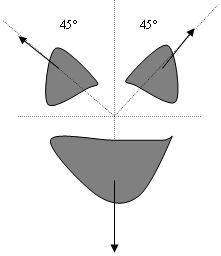
2. momentum initial = momentum final.
Pi=Pf[
M*V+M*V=M*V+M*V



3. I think I need to find the x and y compenents of the smaller 2kg piece, but I don't know how to start because the bigger piece is at 90 degrees. this would make the x compenent 0 right? if i solve for the y direction... M*V+M*V=0 would I take half of the mass of the big ice chunk because it splits evenly? I used 4(2)+2(V)=0 to get a y compenent of 4. then use trig to get the vector velocity which I got to = 5.7 m/s. Is this right?

 

[voko]

It is impossible to understand what you mean because equations like M*V+M*V=M*V+M*V make no sense. They are the same as 1 = 1: always true, but carry no information whatsoever. M*V+M*V=0 is hardly better, because it means V = 0, which cannot be true in this case. Please use notation that let's other people understand what you are doing. You can denote the little piece's mass as m, their velocities as v, and those of the large piece M and V.