2nd Kirchhoff's law for all passive elements

  • Context: Undergrad 
  • Thread starter Thread starter Jhenrique
  • Start date Start date
  • Tags Tags
    Elements Law
Click For Summary

Discussion Overview

The discussion revolves around the application of Kirchhoff's 2nd law to circuits containing passive elements such as inductors, capacitors, and current sources. Participants explore the behavior of these components in relation to the law, particularly in the context of voltage summation around a loop.

Discussion Character

  • Technical explanation
  • Debate/contested
  • Mathematical reasoning

Main Points Raised

  • One participant inquires about the behavior of inductors, capacitors, and current sources with respect to Kirchhoff's 2nd law.
  • Several participants assert that Kirchhoff's 2nd law applies to inductors and capacitors, stating the equation VI + VR + VL + VC = 0, emphasizing the time-dependent nature of voltages.
  • There is a suggestion that adding a voltage source in series modifies the equation to VI + VR + VL + VC = VV.
  • Another participant proposes rewriting the equation as VI + VR + VL + VC - VV = 0, questioning the orientation of the voltage source.
  • One participant expresses a preference for placing potential differences that favor current circulation on one side of the equation and those that oppose it on the other, describing this as intuitive.
  • A later reply advises marking diagrams consistently and summing voltages around loops, noting that unknown voltages may yield unexpected signs.

Areas of Agreement / Disagreement

Participants express differing views on the orientation of voltage sources and the interpretation of potential differences in relation to current circulation. The discussion remains unresolved with multiple competing perspectives on how to apply Kirchhoff's 2nd law in this context.

Contextual Notes

There are unresolved assumptions regarding the orientation of voltage sources and the definitions of potential differences in the context of current flow. The discussion does not reach a consensus on these points.

Jhenrique
Messages
676
Reaction score
4
How would be the 2nd Kirchhoff's law for this circuit here:

attachment.php?attachmentid=70425&stc=1&d=1402186250.png


I'm asking because I don't know how is the behavior of the inductor, capacitor and current source wrt the 2nd Kirchhoff's law...
 

Attachments

  • cc.PNG
    cc.PNG
    1.2 KB · Views: 635
Physics news on Phys.org
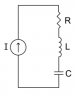
Kirchhoff's 2nd law states that the sum of the voltages around a loop is zero. It also applies to inductors and capacitors so..

VI + VR + VL + VC = 0

The voltage (particularly on Inductors and capacitors) is time dependent but the above still applies at any instant in time.
 
CWatters said:
Kirchhoff's 2nd law states that the sum of the voltages around a loop is zero. It also applies to inductors and capacitors so..

VI + VR + VL + VC = 0

The voltage (particularly on Inductors and capacitors) is time dependent but the above still applies at any instant in time.

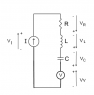
And if I add a voltage source in series in this circuit, the equation will be so:

VI + VR + VL + VC = VV

Yeah!?
 
Jhenrique said:
And if I add a voltage source in series in this circuit, the equation will be so:

VI + VR + VL + VC = VV

Yeah!?

Yeah!
 
  • Like
Likes   Reactions: 1 person
Yes. Although it might be better to write it as..

VI + VR + VL + VC - VV = 0

Did you realize you may have implied a different orientation for the additional voltage source VV?
 

Attachments

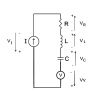
  • attachment.png
    attachment.png
    2.4 KB · Views: 496
Last edited:
or if you prefer
 

Attachments

  • attachment.png
    attachment.png
    2.5 KB · Views: 549
CWatters said:
Yes. Although it might be better to write it as..

VI + VR + VL + VC - VV = 0

Did you realize you may have implied a different orientation for the additional voltage source VV?

CWatters said:
or if you prefer

Interesting and confused!
 
But I don't think so... I place in the left side of the equation the potential difference that favors the circulation of the current and I place in the right side the potential differences opposes the circulation of the current. I can't think in another way more intuitive...
 
It's not always obvious if a "voltage" opposes or increases the current. Best practice is to mark your diagram in a consistent way, then go around each loop summing all the voltages. Then solve any simultaneous equations (eg for circuits with multiple loops). You may well find some unknown voltages turn out -ve when you were expecting them to be +ve.
 

Similar threads

High School Found a circuit where current is zero across an ohmic device (dV>0)
  • · Replies 11 ·
Replies
11
Views
1K
Graduate Battery connected to a pure inductor with a Zero-resistance wire
  • · Replies 10 ·
Replies
10
Views
2K
Undergrad Which law defines the AC inducing voltage in the inductor?
  • · Replies 25 ·
Replies
25
Views
3K
Undergrad Question about Capacitor current and electromagnetic induction
  • · Replies 16 ·
Replies
16
Views
2K
Undergrad What Am I Missing About Kirchhoff's Law in LC Circuits?
  • · Replies 8 ·
Replies
8
Views
6K
Undergrad On the stability of an LTI circuit
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Discharge in a DC RC circuit and Kirchhoff's Loop Rule
  • · Replies 9 ·
Replies
9
Views
4K
Graduate What is Kirchhoff's Current Law
  • · Replies 1 ·
Replies
1
Views
6K
Undergrad How to do the calculations for a Wheatstone Bridge
  • · Replies 15 ·
Replies
15
Views
4K
High School Why do capacitors not discharge everything immediately in LC circuits?
  • · Replies 15 ·
Replies
15
Views
2K