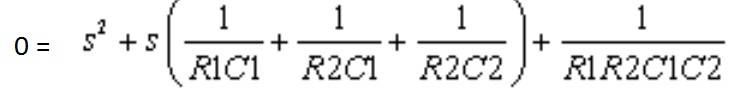Discussion Overview
The discussion revolves around the feasibility of designing a second-order capacitor-resistor (CR) low-pass or high-pass filter (LPF/HPF) with equal cutoff frequencies for both poles. Participants explore theoretical aspects, practical implementations, and the implications of loading effects in filter design.
Discussion Character
- Technical explanation
- Debate/contested
- Mathematical reasoning
- Experimental/applied
Main Points Raised
- Some participants propose that it is theoretically possible to set the poles equal in a second-order filter.
- Concerns are raised about the practicality of passive filters in terms of loading effects, particularly when interfacing with BJT amplifier stages.
- One participant mentions that the filter's response will change due to the loading from the BJT input.
- Another participant suggests that if the filter is designed for a fixed load, that load must be included in the filter equation.
- There is a discussion about the implications of having two equal poles, with one participant expressing doubt about the possibility due to the requirement for complex conjugate pairs in the pole positions.
- Some participants discuss the necessity of using buffer amplifiers to avoid loading issues between filter stages, noting that this may allow for the realization of equal poles.
- A rule of thumb is mentioned regarding the impedance ratios needed between cascaded passive filters to minimize loading effects.
Areas of Agreement / Disagreement
Participants express differing views on the feasibility of achieving equal poles in the filter design. While some believe it is possible under certain conditions (e.g., using buffer amplifiers), others question the practicality and theoretical basis for such an arrangement. The discussion remains unresolved regarding the exact conditions under which equal poles can be achieved.
Contextual Notes
Limitations include the dependence on specific load conditions and the assumptions made in the filter equations. The discussion highlights the complexity of accurately modeling the filter response when accounting for loading effects.