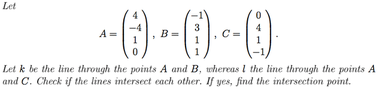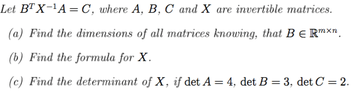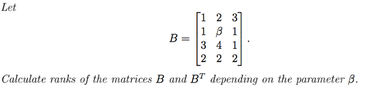namerequired said:
It should be a square matrix and it is the opposite of the original one and has to be determined, so it can't have Det = 0.
Exactly. The information that it is an square matrix is important. Using "opposite" as terminology is not adequate here in my opinion, as I usually associate that word for addition. So consider this: if $B \in \mathbb{R}^{m \times n}$ and $B$ is invertible, then what can you say about $m$ and $n$? This answers more than just $B$: the dimensions of all other matrices are automatically determined.
namerequired said:
det A = Det A^T
The position matter
det(AB) = det(A) and det(B)
for invertible matrices det(A) cannot be 0
You are correct. In order to apply that information you need to isolate $X$ in the equation $B^{T} X^{-1} A = C$. Looking at it, we can see some possible orders to do this. I would do as the following:
1) Eliminate $A$ (how?), transpose what the rest (to eliminate $B$), invert and transpose back.
Any other order is essentially an rearrangement of the above.
namerequired said:
Row operations to find the diagonal, or check if the det of a sub matrix 2x2, 3x3 is not 0
These are correct, but rather tedious. In particular there are many determinants to be computed, so it's not really a good option. What else can we do? This information is important: the rank of the matrix is always less than or equal to the minimum between the number of rows and columns. Let's apply in this case: we have 4 rows and 3 columns, therefore whatever the rank of the matrix is it has to be less than or equal to 3.
How can we check that? Consider the three columns as vectors and make a linear combination of them, equating to zero. From here you should find the condition on $\beta$ that answers the problem.
namerequired said:
I look for the coordinate of the 2 points.
This isn't correct. You already have two points and you want a line between them. The most common way (but definitely not unique) to define such line is to write it as
$$r = \{ P_1 + t(P_2 - P_1), \, t \in \mathbb{R} \}.$$
The parameter $t$ controls where you are in the line. At $t=0$ you start at point $P_1$, while at $t=1$ you are at $P_2$. It is usual to think of it as "time" (hence the letter $t$) and this parametrization of the line as the unit time taken to walk the line leaving one point and arriving at another.
Try using it this time: first write the equations of lines $AB$ and then $AC$. What will be the condition for them to intersect? :)
- Sorry to post more than 2, actually the first question was more a bonus, because I don't really understand if the problem is so easy or so tricky )
