3D geometry parallelepiped problem

Click For Summary
SUMMARY

The discussion centers on proving that points K and L, where the diagonal AG of a rectangular parallelepiped ABCDEFGH intersects planes BDE and CFH, are the centers of gravity for these planes. The user demonstrates the alignment of points A, G1, and G, establishing that K equals G1, and similarly shows that L equals G2. The calculations confirm that K and L are located at one-third and two-thirds along the diagonal AG, respectively, affirming their roles as centers of gravity for the respective planes.

PREREQUISITES
  • Understanding of 3D geometry and vector notation
  • Familiarity with the concept of centers of gravity in geometric shapes
  • Knowledge of the properties of rectangular parallelepipeds
  • Ability to perform vector algebra and geometric proofs
NEXT STEPS
  • Study vector algebra applications in 3D geometry
  • Explore the properties of centers of mass in various geometric shapes
  • Learn about geometric proofs involving intersections of planes and lines
  • Investigate visual representations of 3D shapes to enhance understanding
USEFUL FOR

Students studying geometry, educators teaching 3D spatial reasoning, and anyone interested in vector mathematics and geometric proofs.

geoffrey159
Messages
535
Reaction score
68

Homework Statement


[/B]
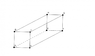
Given a rectangular parallelepiped ABCDEFGH, the diagonal [AG] crosses planes BDE and CFH in K and L. Show K and L are BDE's and CFH's centres of gravity.

I think I have understood the problem, could you verify my demo please ? Thanks

Homework Equations



The Attempt at a Solution



Let us call ##G_1## and ##G_2## BDE's and CFH's center of gravity.

## \vec{AG} = \vec{AB} + \vec{AD} + \vec{AE} = 3 \vec{AG_1}##

So ## A,G_1, G## are aligned and ##G_1## belongs to plane BDE so we must have ##K = G_1##

Then

## 3 \vec{AG_2} = \vec{AC} + \vec{AF} + \vec{AH} = \vec{AB} + \vec{BC} + \vec{AE}+\vec{EF} + \vec{AD} + \vec{DH} = \vec{AG} + \vec{BC} + \vec{EF}+\vec{DH} = 2\vec{AG}##

So, similarly, ## A,G_2, G## are aligned and ##G_2## belongs to plane CFH so we must have ##L = G_2##

Furthermore, ##K## and ##L## are at the third and two third of the diagonal.
 
Physics news on Phys.org
It would help if you provided a picture of your regular parallelepiped with vertices labeled.
 
Hi, here is the picture
 

Attachments

  • drawing.png
    drawing.png
    20.8 KB · Views: 323

Similar threads

Graduate What Does Mathematical Sameness Mean?
  • · Replies 7 ·
Replies
7
Views
3K