9-point Laplacian stencil derivation

[NicolaiTheDane]

TL;DR Summary

can someone show me how?

Hey there

I'm currently taking a course on numerical methods for solving differential equations, and atm we are working with the discrete laplacian operator. In particular the 9-point stencil:

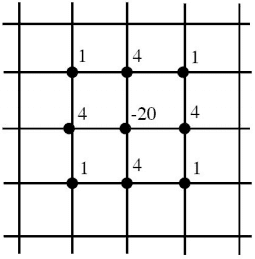
However unlike the 5-point stencil, this one is getting to me. I have tried several things, in order to derivate it, but nothing works. Method of undetermined coefficients doesn't work, because no solution allows for the cancellation of all the undesired derivative terms of the Taylor expansions (All the even derivative terms, have the same coefficient composition). My book " Finite Difference Methods for Ordinary and Partial Differential Equations. " by Randall J. LeVeque merely states that is works, and searching the internet doesn't lead to any clarity either.

Can someone explain to me, how derivate it?

 

[Paul Colby]

I can't derive it the way you are with Taylor series but it's interesting that the stencil you give is a weighted sum of two 5 point stencils. Looking at the grid horizontally and vertically, $$\partial_x^2 \simeq (f_{1,0}-2f_{0,0}+f_{-1,0})\frac{1}{h^2}$$ $$\partial_y^2 \simeq (f_{0,1}-2f_{0,0}+f_{0,-1})\frac{1}{h^2}$$
add these together gives the usual 5-point stencil, say $\nabla_1^2$. Okay, rotate your head and look at the 45 degree diagonals. This gives the 5-point stencil $\nabla_2^2$ where $h$ is now $\sqrt{2}h$. The stencil you give is,

$$\nabla^2 = 4\nabla_1^2 + \nabla_2^2$$

which I think is off by a factor of 5.

 

[NicolaiTheDane]

I can't derive it the way you are with Taylor series but it's interesting that the stencil you give is a weighted sum of two 5 point stencils. Looking at the grid horizontally and vertically, $$\partial_x^2 \simeq (f_{1,0}-2f_{0,0}+f_{-1,0})\frac{1}{h^2}$$ $$\partial_y^2 \simeq (f_{0,1}-2f_{0,0}+f_{0,-1})\frac{1}{h^2}$$
add these together gives the usual 5-point stencil, say $\nabla_1^2$. Okay, rotate your head and look at the 45 degree diagonals. This gives the 5-point stencil $\nabla_2^2$ where $h$ is now $\sqrt{2}h$. The stencil you give is,

$$\nabla^2 = 4\nabla_1^2 + \nabla_2^2$$

which I think is off by a factor of 5.

I see. I wouldn't have thought of trying that route.

However! I succeed by substituting all the Taylor expansions, despite it being an extreme amount of grunt work, and then using method of undetermined characteristics. The key was to realize, that I wanted the operator to have a specific error: $$\nabla^{2}_{9}u = \nabla^{2}u + \frac{h^2}{12}(u_{xxxx}+2u_{xxyy}+u_{yyyy})+O(h^4)$$

Once I realized this, solving the system for the desired coefficients, yield the values I was looking for. Since $$u_{xxxx}+2u_{xxyy}+u_{yyyy} = \nabla^{2}(\nabla^{2}u) = \nabla^{2}f$$
all I had to do, to get the desired convergence rate, was to correct the right hand side.

Thanks again though!

 

[Paul Colby]

One question. What happened to the factor of 5 over estimate for $\nabla^2$? Seems to me yours is $5\nabla^2$?

 

[NicolaiTheDane]

One question. What happened to the factor of 5 over estimate for $\nabla^2$? Seems to me yours is $5\nabla^2$?

Well I don't derive it like you did. Instead wrote an equation, where the coefficients are unknown:
$$\nabla^{2}_{9}u =c_1U_{i+1,j+1}+c_2U_{i+1,j}+c_3U_{i+1,j-1}+c_4U_{i,j+1}+c_5U_{i,j}+c_6U_{i,j-1}+c_7U_{i-1,j+1}+c_8U_{i-1,j}+c_9U_{i-1,j-1}$$

Then taking the Taylor expansion of all the U's and factorizing each term, such that it depends on a combination of those coefficients, I can "pick" which terms survives, and which gets canceled out.

If I only wanted the pure second order derivatives to survive, I would get the the coefficients for the standard 5 point stencil (that is, the diagonal U's disappear). However if I deliberately choose to keep those which produce the error I showed earlier, I get the correct coefficients. It was very tedious to setup, and I used Maple to make sure I didn't make any errors. I can upload it if you like, but it isn't pretty.

LINK: https://file.io/4lgGxFTJYFXy

Keep it mind, it is just notes, and wasn't intended for anyone but me.

 

[Paul Colby]

Hey, thanks. My only thought is that applying $\nabla^2_5$ and $\nabla^2_9$ to some second order polynomial like $x^2+y^2$ should give something on the order of 4 for both. This clearly doesn't happen for $\nabla^2_9$. Am I missing something?

 

[Paul Colby]

So, I programmed these two stencils up in MAXIMA. $\nabla^2_5$ gives 4 when applied to $x^2+y^2$ at any point $(x,y)$ while $\nabla^2_9$ gives 24 anywhere in the plane. I would suggest dividing the stencil $\nabla^2_9$ as you've given it by 6, not 5.

 

[BvU]

LINK: https://file.io/4lgGxFTJYFXy

Keep it mind, it is just notes, and wasn't intended for anyone but me.

Is that the reason your link is a dud ? :

 

[Paul Colby]

I successfully downloaded it, installed maple to read it. Didn’t get very far and was unable to find his missing factor.

 

[NicolaiTheDane]

Is that the reason your link is a dud ? :
View attachment 280281

Must have been a short lived link. I don't usually need to upload for public use, so I just took the first and best google suggestion.

I successfully downloaded it, installed maple to read it. Didn’t get very far and was unable to find his missing factor.

What missing factor? Also keep in mind, that the Maple ark was merely a simple way, for me to check how those coefficients comes up. The actual implementations that I use for my university course, is done in Matlab. If you tell me what you want me to test, or show you, I'll be happy to provide it.

 

[Paul Colby]

What missing factor?

Well, let’s work it out. Try an example that should be exact because there are fewer terms present than the stencil accommodates. Take $$f(x,y)=x^2+y^2$$ Clearly the exact result is $$\nabla^2f=4$$ The 5 point stencil also yields 4 as it should. The nine point stencil you posted yields 24 as the result. QED

 

[NicolaiTheDane]

Well, let’s work it out. Try an example that should be exact because there are fewer terms present than the stencil accommodates. Take $$f(x,y)=x^2+y^2$$ Clearly the exact result is $$\nabla^2f=4$$ The 5 point stencil also yields 4 as it should. The nine point stencil you posted yields 24 as the result. QED

Ahhh my apologies! The coefficients in the picture is not the correct coefficients, but merely the coefficients not dependent on the step size. If you want to use those coefficients, then you have to multiple all of them by 1/h^2 in the case of the 5-point stencil, and 1/(6*h^2) for the 9-point stencil. In the case of h = 1 (which is the case you have been assuming because I left out some crucial information), then we correct by multiplying 1/6 * 24 = 4 :)

Sorry being obscure.

 

[Paul Colby]

because I left out some crucial information

It’s taken me 5 fairly direct posts to get to this point. I need to work on my non replies.