mech-eng
- 825
- 13
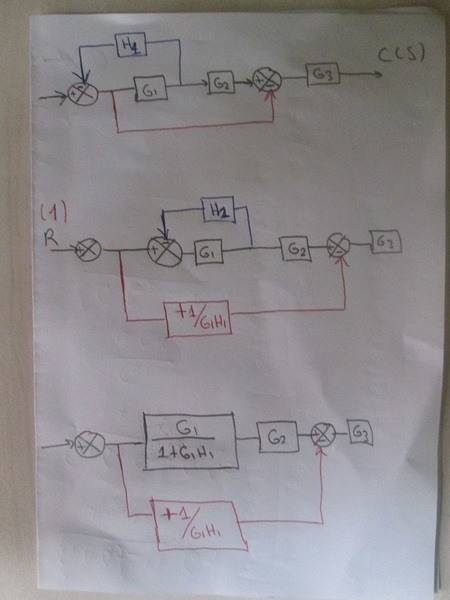
I try to solve a block diagram reduction example but when I did the operations, sign of one operation is incorrect. I tried to understand why it is so? Would somebody like to help me.
(1) First I carry the feedback into the parallel line.
(2) I add +1/G1H1 in the parallel line because I thought the orinal signal is that signal entering the parallel line.
3) I did serial and parallel operations but the result is incorrect by just a sign.
T(s)=G3 +G1G2G3/1+G1H1 which is the correct answer.
But the result I found by myself is
T(s)=-G3+G1G2G3/1+G1H1 which is the wrong answer by a sign.
Thank you.
(1) First I carry the feedback into the parallel line.
(2) I add +1/G1H1 in the parallel line because I thought the orinal signal is that signal entering the parallel line.
3) I did serial and parallel operations but the result is incorrect by just a sign.
T(s)=G3 +G1G2G3/1+G1H1 which is the correct answer.
But the result I found by myself is
T(s)=-G3+G1G2G3/1+G1H1 which is the wrong answer by a sign.
Thank you.