uzair_ha91
- 92
- 0
A.C. Circuits -- Graphs
http://img136.imageshack.us/img136/5782/image64.jpg
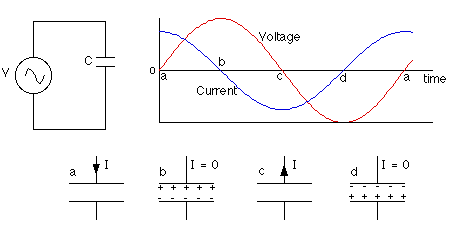
In this graph, the curve of current is larger than that of voltage...but in some books the voltage curve is above the current curve (like the one below)...Which one's correct?
http://img136.imageshack.us/img136/5782/image64.jpg
In this graph, the curve of current is larger than that of voltage...but in some books the voltage curve is above the current curve (like the one below)...Which one's correct?
Last edited by a moderator: