ucsbjosh
- 1
- 0
a couple of "basic" physics problems
i am stuck on a couple of my homework problems for my "basic" physics class. any help with either of them would be greatly appreciated.
1. a window washer pulls herself up in a bucket-pulley apparatus (single massless, frictionless pulley). how hard must she pull downward (on the rope end) to raise herself slowly at constant speed? the mass of the person and the bucket is 67 kg.
i am not sure how to get started on this problem, i think that the bucket is being pulled down by gravity with the force mg, and that to slowly raise herself at a constant speed she would need to pull with slightly more force than that, but i can't seem to get the right answer.
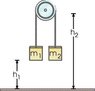
2. the two masses, m1 = 2.10 kg and m2 = 3.20 kg shown in the figure below, are each initially h1 = 1.56 m above the ground, and the massless, frictionless pulley is fixed h2 = 4.84 m above the ground. suppose the pulley is suspended by a cord to the ceiling. what is the tension in this cord after the mass is released and before it hits the ground? (i have attached the figure)
when i try to work this problem, i understand that the masses are both accelerating at the same rate, with m1 going up (y+) and m2 going down (y-) and that while they are in this state, they put a force downward on the pulley, which in turn puts a tension into the rope. i am not sure how to find the tension in that rope that is suspending the pulley from the ceiling.
again, any help with either of these problems would be greatly appreciated, thanks in advance.
josh
i am stuck on a couple of my homework problems for my "basic" physics class. any help with either of them would be greatly appreciated.
1. a window washer pulls herself up in a bucket-pulley apparatus (single massless, frictionless pulley). how hard must she pull downward (on the rope end) to raise herself slowly at constant speed? the mass of the person and the bucket is 67 kg.
i am not sure how to get started on this problem, i think that the bucket is being pulled down by gravity with the force mg, and that to slowly raise herself at a constant speed she would need to pull with slightly more force than that, but i can't seem to get the right answer.
2. the two masses, m1 = 2.10 kg and m2 = 3.20 kg shown in the figure below, are each initially h1 = 1.56 m above the ground, and the massless, frictionless pulley is fixed h2 = 4.84 m above the ground. suppose the pulley is suspended by a cord to the ceiling. what is the tension in this cord after the mass is released and before it hits the ground? (i have attached the figure)
when i try to work this problem, i understand that the masses are both accelerating at the same rate, with m1 going up (y+) and m2 going down (y-) and that while they are in this state, they put a force downward on the pulley, which in turn puts a tension into the rope. i am not sure how to find the tension in that rope that is suspending the pulley from the ceiling.
again, any help with either of these problems would be greatly appreciated, thanks in advance.
josh