brotherbobby
- 766
- 171
- Homework Statement
- For a triangle ##\text{ABC}##, prove that $$\boxed{\cos A+\cos B+\cos C-1=\dfrac{a^2b+b^2c+c^2a+b^2a+c^2b+a^2c-a^3-b^3-c^3-2abc}{2abc}}$$
- Relevant Equations
- 1. ##\cos\frac{A}{2}= \sqrt{\dfrac{s(s-a)}{bc}}## and its cyclic counterparts.
2. ##\sin\frac{A}{2}= \sqrt{\dfrac{(s-b)(s-c)}{bc}}## and its cyclic counterparts.
3. ##s=\dfrac{a+b+c}{2}##, the semi perimeter of a triangle.
Problem Statement : The statement appeared on a website where a different problem was being solved. I got stuck at the (first) statement in the solution that I posted above  . Here I copy and paste that statement from the website, which I cannot show :
. Here I copy and paste that statement from the website, which I cannot show :
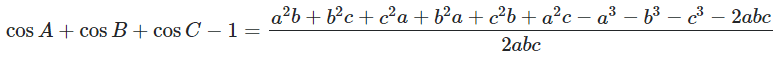
Attempt : To save time typing, I write out and paste the solution using Xournal++, hoping am not violating anything.
 Issue : As evidence by the coefficients that I have marked in red, my answer is not the same as that shown for the problem.
Issue : As evidence by the coefficients that I have marked in red, my answer is not the same as that shown for the problem.
A hint as to where I went wrong would be welcome.
Attempt : To save time typing, I write out and paste the solution using Xournal++, hoping am not violating anything.
A hint as to where I went wrong would be welcome.