- #1
- 42,989
- 975
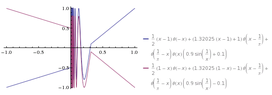
Find two sets P and Q satisfying
I) P and Q are completely contained in the square, in R2, with vertices (1, 1), (1, -1), (-1, -1), and (-1, 1).
II) P contains the ponts (1, 1) and (-1, -1) while Q contains (-1, 1) and (1, -1).
III) P and Q are disjoint.
IV) P and Q are both connected sets.
I) P and Q are completely contained in the square, in R2, with vertices (1, 1), (1, -1), (-1, -1), and (-1, 1).
II) P contains the ponts (1, 1) and (-1, -1) while Q contains (-1, 1) and (1, -1).
III) P and Q are disjoint.
IV) P and Q are both connected sets.