A hard question from the Oxford interview

[Negi Magi]

Homework Statement

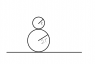
See the attached picture.
The big disk is fixed on the ground, and the small disk move under the gravity. There is no friction between two disks. When will the small disk is no longer touch the big disk? Just measure the distance between the center of the small disk and the ground.

Homework Equations

The conservation of the energy
The equation of the circular motion

The Attempt at a Solution

I just consider that the centripetal force on the small disk, which is one of the component of the gravity on the small disk, may be the key to answer this question. But I really don't know how to write it into an equation and to solve it

 

[mfb]

For a given velocity v, you can calculate the centripetal force required to keep the disk sliding. Gravity has to provide this force (but pay attention to its direction).

 

[Basic_Physics]

Since there is no rolling the potential energy is just converted into kinetic energy. The speed will be tangential to the line connecting it to centre of the big disc. One can simplify it by considering a point mass at 3r following a circular path. The component of g along the line to the centre of the big disc provides the centripetal acceleration.