A layman's guide to the accelerating expansion of space

[valenumr]

I am writing this thread because I have too often had to explain this and I basically wanted to have a resource available to direct folks to, and, frankly, the Wikipedia topics on this are pretty vague on the explanation. Any questions, comments, or corrections are greatly appreciated. So, here we go...

Often, the argument is made that the expansion of the universe must be decelerating which is incorrect. The first argument is that more distant galaxies are receding more quickly than nearer galaxies, while the second is that more distant galaxies are older than nearer galaxies. While both statements are scientifically accepted, the conclusion that galaxies were recessing faster in the past and therefore the expansion of the universe is decelerating is completely incorrect.

Another incorrect assumption often made is that this expansion, which leads to the recession of distant galaxies, is equated with proper relative motion, and that the galaxies have a relative velocity component due to this recession. This also is not correct. It is more appropriate to consider that galaxies remain fixed, with the empty space between expanding over time. Certainly, there can be true relative motion among galaxies, and it would be quite unphysical if there were not.

Before you can convince yourself or anyone else that the expansion of the universe is, in fact, accelerating, you first must understand how the universe would appear to a fixed observer if the expansion rate were constant. I will attempt to explain this as clearly as possible.

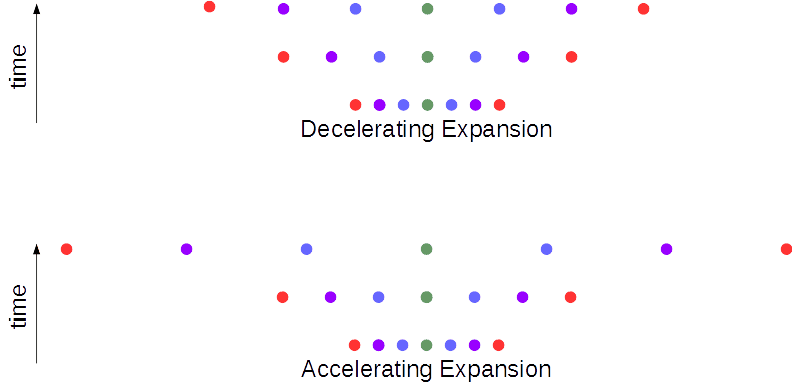
The above diagram illustrates how this constant rate expansion would occur in a single spatial dimension for seven uniformly spaced galaxies over two time intervals, with time progressing from bottom to top. The green dots represent a fixed observer galaxy, while the blue, purple, and red dots represent progressively more distant galaxies. So initially the blue galaxies are 1 unit away, the purple galaxies are 2 units away, and the red galaxies are 3 units away.

After one time interval, the configuration of the galaxies is now such that the blue galaxies are 2 units away, the purple galaxies are 4 units away, and the red galaxies are 6 units away, so space has expanded uniformly to twice it's original size. But notice that the change in distance from the fixed, green observer is progressive: the blue galaxies have recessed by 1 unit, the purple by 2, and the red by 3! Now it should be clear that this change in distance is directly proportional to the observed distance, which in this case, the ratio is 1/2.

As mentioned above, this change of distance is entirely different from physical motion, and it should be clear from the diagram that it is happening very uniformly at any instant in time. Space is not expanding faster anywhere regardless of distance. The fact that distant galaxies appear to be receding faster is entirely an observer effect due to the fact that there is more space between an observer and a more distant galaxy.

Finally, after a second interval of time, we can see in the diagram that the space between all galaxies has again doubled uniformly, so this is how constant expansion would appear to our fixed observer over time. The blue galaxy is now 4 units away, the purple 8, and the red 12. But again notice that the change in distance is progressive, directly proportional to the observed distance, and that the ratio is still 1/2, which demonstrates that, at least in this scenario, the rate of expansion is constant.

So now that we understand the expansion of the universe more clearly, how can we determine if the rate of expansion is decreasing, constant, or, increasing? Well, we can take the top line of the diagram and either slightly stretch it (accelerating expansion) or slightly compress it (decelerating expansion). Now I'll leave it to you to deduce the observational effects of either case, but remember while doing so, that we can only observe the present (galaxies in the top line of the diagram). Hint: red-shift is cumulative over time.

As a final note, scientists used this same process to search for evidence that this expansion was slowing down due to gravitational effects. They made specific predictions so they would know where to search, and their observations actually demonstrated the opposite of what was expected. Granted there is still a lot of debate over the accuracy of the measurements and variety of other factors involved in these experiments, but the tide seems to be in favor of accelerating expansion. Sorry Dark Energy Haters.

 

[phinds]

... the tide seems to be in favor of accelerating expansion. Sorry Dark Energy Haters.

I think putting it that way makes the case MUCH less strongly than it should be made. It's not a "tide in favor of" it's an "overwhelming tidal wave" of evidence. Accuracy can be debated, but that's quantitative detail. The qualitative results are, I believe, indisputable at this point.

 

[valenumr]

I think putting it that way makes the case MUCH less strongly than it should be made.

Just trying to keep it objective. I would say there is at least a minority effort to refute the claim, and there is an ongoing effort to strengthen its support as well. I do agree that general consensus accepts accelerating expansion as indisputable given our present understanding.

 

[Bandersnatch]

the conclusion that galaxies were recessing faster in the past and therefore the expansion of the universe is decelerating is completely incorrect.

It's not completely incorrect. For a good part of the history of the universe the expansion was indeed decelerating. Look up evolution of the scale factor.

 

[marcus]

... For a good part of the history of the universe the expansion was indeed decelerating. Look up evolution of the scale factor.

It's a good suggestion, to look up the evolution of the scale factor. When you solve the equation of the standard cosmic model (which basically everybody uses) you get a scale factor curve that looks like the righthand side of this plot

The time scale is 1 = 17.3 billion years.
The present age is 0.8 = 13.8 billion years.
You can see that the deceleration lasted until around age 0.44.
It is very subtle but after 0.45 it the size of distances begins to "accelerate" in the sense that the scale factor slope increases.

You can calculate this curve, the universe's distance growth curve, yourself using google calculator. Anyone can.
It is simply the hypersine "sinh" raised to the 2/3 power

the usual notation for the scale factor is a(t) so the equation is $$a(t) = \sinh^{2/3}(\frac{3}{2}t)$$ for convenience it is customary to divide this by its present value to "normalize" it so that it equals ONE at present age. So you divide that by 1.3 or more precisely 1.3115. and then a(now) = 1
What I have plotted here is $$a(t) = \frac{\sinh^{2/3}(\frac{3}{2}t)}{1.3115}$$ You can see that at the present age, t = 0.8, you have a(.8) = 1

 

[eltodesukane]

[...] Now I'll leave it to you to deduce the observational effects of either case, but remember while doing so, that we can only observe the present (galaxies in the top line of the diagram). Hint: red-shift is cumulative over time.

I don't understand.
"We can only observe the present", but looking far away we see into the past.
So if we are the green dot on the top line, we can see the blue dot on the 2nd line, the purple dot on the 3rd line, and the red dot on the missing 4th line.
In both case we observe the same thing, no acceleration or deceleration.

 

[valenumr]

It's not completely incorrect. For a good part of the history of the universe the expansion was indeed decelerating. Look up evolution of the scale factor.

Fair enough, but that is out of context. Perhaps I should have worded that better. My point is, the conclusion that the expansion is decelerating now based on the two stated premises is completely incorrect.

My point is really to illustrate how constant expansion leads to Hubble's law without getting into too much math.

 

[valenumr]

"We can only observe the present", but looking far away we see into the past.

Both statements there are true in their own way. We can only observe the light arriving at the present from distant sources, but we know it was emitted in the past. As a gross simplification, think of the top line as what we observe at present, and the two bottom lines as two different alternate histories as to how the universe evolved to the "present", with each history leading two different observations.

This is actually one aspect of cosmology that blows my mind though. When we look out to the edge of the observable universe in opposite directions, we can say that those two regions are very far from each other. But when light from those regions was emitted, they were much closer together. Looking outward into space is like looking inward into the past.

 

[phinds]

Looking outward into space is like looking inward into the past.

Well, actually, it's not "like" looking into the past, it IS looking into the past.

 

[marcus]

My comment would be that the detection of a cosmological constant was based, as we know, on redshift-distance data on standard candle supernovae. For a given redshift (1+z is the wavelength enlargement factor, which is also the distance enlargement while the light was in transit) the standard supernovae proved to be DIMMER.
SO MORE DISTANT than was expected, given the amount of expansion that had occurred while the light was traveling.

turn that around and it says for standard sources observed at a given distance, there has been LESS DISTANCE EXPANSION RECENTLY while the light was coming to us. Less redshift, for a given distance. than would have been expected with zero cosmo. const.

Because more distance (more dimness) for a given redshift than you'd get with zero cosmological constant.

that seems contradictory, paradoxical. It does not seem to compat in a simple way with our verbal description and our naive mental image of "acceleration"
====================

I don't know of a simple verbal explanation that makes this intuitive. Maybe someone else here can explain. I think you have to address how we actually SEE the positive Lambda in the plot that compares redshift to luminosity (dimness----i.e. distance).

you have to tackle the fact of what is observed

after all, we don't actually SEE things "accelerating". we can't even watch things "move away" because distances expand so slowly (in human terms)
currently 1/144 of one percent in a million years.

and redshift is not a DOPPLER effect of some "speed" at a particular moment like when the light was emitted. It is so important to realize that!
It is not related to any particular "speed" at any particular moment. Cosmological redshift measures the entire cumulative effect of all the expansion over the whole time the light was in transit. This is not related in any simple way to the recession speed at any given moment.
====================

So my feeling is that it is not trivial to try to explain the effect on observations of a positive cosmo. const. Lambda.

Probably the first fact to grasp is what the Hubble expansion rate H(t) represents and to realize that it has been DECLINING since very early times and according to standard cosmology it is expected to CONTINUE declining.

this is the key fact, how H(t) is declining. People often get the idea from all the "expansion" and "dark energy" talk that it must be increasing, but this is a confusion.

 

[eltodesukane]

..When we look out to the edge of the observable universe in opposite directions, we can say that those two regions are very far from each other. But when light from those regions was emitted, they were much closer together.

Yes, and if we could look further to the time of the Big Bang (which we can not cause the universe becomes opaque to light at a certain point), those two regions would actually be at the same location. (which is why I don't understand why inflation is said to be necessary to causally link these two regions).

 

[valenumr]

turn that around and it says for standard sources observed at a given distance, there has been LESS DISTANCE EXPANSION RECENTLY while the light was coming to us. Less redshift, for a given distance. than would have been expected with zero cosmo. const.

Is it possible that there is a greater effect of gravitation nearby, or has this already been accounted for or otherwise considered and rejected?

 

[valenumr]

Yes, and if we could look further to the time of the Big Bang (which we can not cause the universe becomes opaque to light at a certain point), those two regions would actually be at the same location. (which is why I don't understand why inflation is said to be necessary to causally link these two regions).

For the first part of your statement, that would have to assume the universe is finite in extent, which is unknown.

Regarding inflation, think of it this way. We are barely causally connected to these two regions at present. But if you think about it, without inflation, they never have been, but perhaps would be sometime in the future.

 

[valenumr]

and redshift is not a DOPPLER effect of some "speed" at a particular moment like when the light was emitted. It is so important to realize that!
It is not related to any particular "speed" at any particular moment. Cosmological redshift measures the entire cumulative effect of all the expansion over the whole time the light was in transit. This is not related in any simple way to the recession speed at any given moment.

Yes, I think this is a common misconception, which I tried to articulate:

Another incorrect assumption often made is that this expansion, which leads to the recession of distant galaxies, is equated with proper relative motion, and that the galaxies have a relative velocity component due to this recession. This also is not correct. It is more appropriate to consider that galaxies remain fixed, with the empty space between expanding over time. Certainly, there can be true relative motion among galaxies, and it would be quite unphysical if there were not.

 

[marcus]

Is it possible that there is a greater effect of gravitation nearby, or has this already been accounted for or otherwise considered and rejected?

All this stuff works out with standard 1915 Einstein GR gravity when you put it in equation terms. Nothing exotic like modified gravity. The seeming unintuitive contradictions come when you try to explain in words. Or when you picture distance expansion as things "moving". Like you said, it is not things moving thru space

Another incorrect assumption often made is that this expansion, which leads to the recession of distant galaxies, is equated with proper relative motion, and that the galaxies have a relative velocity component due to this recession. This also is not correct. It is more appropriate to consider that galaxies remain fixed, with the empty space between expanding over time. Certainly, there can be true relative motion among galaxies, and it would be quite unphysical if there were not...

good point.

 

[eltodesukane]

For the first part of your statement, that would have to assume the universe is finite in extent..

No, but we still can not see beyond that Big Bang distance because the light beyond it had no time to reach us. So the universe beyond that is inaccessible to us, whether it is finite or infinite.

 

[valenumr]

No, but we still can not see beyond that Big Bang distance because the light beyond it had no time to reach us. So the universe beyond that is inaccessible to us, whether it is finite or infinite.

Actually, we can see the CMB, which is essentially the radiation from the surface of last scattering. There is nothing visible before this, because according to theory, the universe was opaque.

 

[marcus]

How the redshift-distance observation data turns into positive Lambda is still a bit unintuitive at least I think so. Maybe someone else can help intuitize it.
As I see it, at the moment, the key thing is a CHANGE OF VARIABLE OF INTEGRATION (just a Freshman college calculus thing, but still a mental obstacle at the most basic level). Distance now (i.e.dimness) is after all an INTEGRAL of the expansion while the light was traveling.

You know the scale factor a(t) that I graphed earlier.

$$D_{now} = \int_{then}^{now} \frac{cdt}{a(t)}$$

this is the integral you first have to understand and then do the change of variable on.

to understand is easy. a(t) is normalized to be 1 at present, so 1/a(t) is the factor by which the little bit of distance cdt is expanded by the time it gets to us.
then is when emitted
now is when received
so you add up all those little steps taken at all different times, and each is multiplied by how much it got expanded during transit.

 

[valenumr]

All this stuff works out with standard 1915 Einstein GR gravity when you put it in equation terms. Nothing exotic like modified gravity. The seeming unintuitive contradictions come when you try to explain in words. Or when you picture distance expansion as things "moving". Like you said, it is not things moving thru space

I think I understand... I guess on the scale that the effects of expansion can be observed, gravity can be essentially ignored due to homogeneity. Would that be accurate?

 

[marcus]

I think so.
I want to tell you what I think is the key step in understanding the dependence of the redshift-distance curve on the positive cosmo curvature constant Lambda.
Are you all right with:

$$D_{now} = \int_{then}^{now} \frac{cdt}{a(t)}$$?

A nice thing is you can define a variable S = 1/a = z+1 called the stretch factor, the factor by which wavelengths and distances got stretched between then and now, while the light was in transit.
And then you can change variable:
$$D_{now} = \int_1^S \frac{ds}{H(s)}$$

where H(s) is the Hubble expansion rate, which we can write as a function of s.

 

[valenumr]

I want to tell you what I think is the key step in understanding the dependence of the redshift-distance curve on the positive cosmo curvature constant Lambda.
Are you all right with

Absolutely. If a(t) is a constant, then everything would look the same regardless of distance (integrating a constant). This doesn't match observation.

 

[valenumr]

I think part of the challenge is what we mean by "now" and "then". I mean, in a sense there is a universal now everywhere, but we only can see "here and now", and everything else is "then and there". But if we could magically teleport 20 billion light years away to "there and now" everything would still pretty much look the same.

 

[marcus]

the secret is that positive Lambda makes H(t) decline more slowly with increasing time, and since S increases as you go BACK in time a positive Lambda makes 1/H(s) decline more slowly with increasing s.
So with positive Lambda you get a bigger integral ds, a bigger distance, a dimmer supernova. It fits the data better!
I don't have time to explain better right now. Here are some H(s) curves for different cosmo const. Lambda. the black one is right, it gives bigger distances (areas under the curve) than the orange one, which is essentially for zero LAMBDA.

 

[marcus]

There is more explanation of those 1/H(s) curves in
https://www.physicsforums.com/threa...iverse-from-observations.814700/#post-5123520
they are on post #3 of that thread

 

[marcus]

If you want to know what Lambda is, really, in terms of actual observations and fitting model parameters to data,
it is given by the longterm value of H(t)
As Einstein introduced Lambda in the GR equation in 1917 it is a RECIPROCAL AREA (a curvature constant in the GR equation)
So if you multiply by c² you get reciprocal time-squared. the square of a growth rate
Λc² is a Time^-2 quantity, per second² or per year²,
whatever time unit you are using.

As t →∞, H(t) → H_∞, the longterm expansion rate and
H_∞² = Λc²/3
So it's simple. If Λ is zero (the way most people thought before 1998) then H declines to zero.
If Λ is some positive curvature constant, then H does not decline all the way to zero.

It levels out at a positive rate H_∞

If Λ is positive the H(t) curve is not so steep

and if you run it backwards in time it is not so steep increasing, so 1/H is not so steep declining.
And increasing S is going backwards in time. So you can see in the plot of 5 sample curves.
The black one (which is right) does not decline so steeply with increasing S.

So integrating, taking area under it, gives larger distances, and that is what they found in 1998.
They found dimmer supernovas than they would have expected using the ORANGE curve, which is for a tiny Lambda almost zero.

But the black curve is just right. If you go to the green one above it, labeled 16.3, you get distances that are too big. the green curve declines TOO slowly.

 

[valenumr]

Marcus,

Just to clarify here, what I was attempting to accomplish was to introduce some very basic topics regarding spatial expansion using a very simple model (constant lambda) to demonstrate the observational effects without requiring any more math than basic arithmetic, while also avoiding ambiguous terminology to confuse expansion with motion, and to specifically address the two misconceptions stated at the top of the first post.

 

[marcus]

Me too, I am trying to help you get it right. I think what I'm offering here is the minimum math version that makes sense of the dependence of the redshift-distance relation on the constant Lambda.

"a very simple model (constant lambda)"

constant Lambda is not a simplification really. There is no evidence that Lambda is changing. (or that it is related to something we'd ordinarily call an "energy". ) It is just a reciprocal area constant that Einstein introduced into GR in 1917

The point I'm making is that we do not observe acceleration. We do not even observe expansion happening. So drawing pictures of expansion and acceleration doesn't get to the heart of it.

what we observe is the redshift-distance relation, exhibited by Type1A supernovae. It would be good to find a plot of that. That is what we have to relate, ultimately, to Lambda.

The question to answer is How does the redshift-distance data relate to the curvature Lambda (i.e. to the longterm value of the Hubble rate). And the goal should be to explain how those data relate to Lambda, or to the longterm Hubble rate that the actual rate is declining towards, with the least possible MATH and the most possible INTUITION.

It's a worthy goal : ^)

Maybe you should find a picture of the redshift-distance data, for starters. There should be a plot in a paper by Perlmutter et al. around 1998. Maybe somebody else can give us a link.
they usually plot it as redshift versus inverse luminosity (dimness.)

The intuitive question is "why were the standard candles dimmer than expected, for a given redshift?"

 

[valenumr]

"a very simple model (constant lambda)"

What I meant was a(t) = k for all time. That's not the case, but it makes it easier, I think, to explain some basic concepts of expansion so there is a clear understanding of the predictions of that model and what they mean before trying to wrap one's head around more complicated models. Also, I really want to talk about it without discussing how we measure those values (red shift vs. sn1a brightness) or parameters like H0, or as you give H(s).

 

[valenumr]

And I have to run for now, but let me reiterate a key point (WRT the overly simplified model): The purpose is to demonstrate why galaxy b appears to recess twice as fast as galaxy a when galaxy b is twice as far away, but in fact everything is just recessing from everything else uniformly. If the scale factor were unchanging over time, there would be a constant ratio of distance to apparent rate of recession.

 

[rootone]

I think that's what people are saying when they say that the shape of the macroscopic universe appears to be flat, (or damn close to flat),

 

[phinds]

Yes, and if we could look further to the time of the Big Bang (which we can not cause the universe becomes opaque to light at a certain point), those two regions would actually be at the same location. (which is why I don't understand why inflation is said to be necessary to causally link these two regions).

No, they most emphatically would not. They wouldn't be very far apart but if they had been at the same point then, they would be at the same point now.

 

[marcus]

What I meant was a(t) = k for all time. That's not the case, but it makes it easier, I think, to explain some basic concepts of expansion so there is a clear understanding of the predictions of that model and what they mean before trying to wrap one's head around more complicated models. Also, I really want to talk about it without discussing how we measure those values (red shift vs. sn1a brightness) or parameters like H0, or as you give H(s).

There may be some small conceptual/notation problems here, but the basic aim is good!

 

[eltodesukane]

No, they most emphatically would not. They wouldn't be very far apart but if they had been at the same point then, they would be at the same point now.

In any case, that same location would be a point, a singularity, which is of course a red flag, showing that our model is not valid there.

 

[phinds]

In any case, that same location would be a point, a singularity, which is of course a red flag, showing that our model is not valid there.

No, it would not. "singularity" does not MEAN "point", it JUST means "the place where our model breaks down and gives unphysical results" and it is not meant to be interpreted as "a point". The choice of the term "singularity" is unfortunate since it gives rise, for you and thousands of other people, to the belief that the universe started as a point and an explosion, and that mistake is pretty much universally repeated in pop-science.

I've even heard it said on TV by respectable scientists who would NEVER say that in a physics class or a formal lecture

 

[marcus]

Yes, and if we could look further to the time of the Big Bang (which we can not cause the universe becomes opaque to light at a certain point), those two regions would actually be at the same location. (which is why I don't understand why inflation is said to be necessary to causally link these two regions).

This puzzlement certainly makes sense to me. We could try to discuss it here, or make a separate thread.
Phinds, maybe Elto already understands some of the points you are trying to get across (like "singularity" does not simply mean "point"). I'm not sure, there could be just a semantic disconnect.

Two distant regions now at opposite sides of the sky seem to be the same temperature, as if they were once in equilibrium. that is said to require something like inflation to have happened. Elton says "why?" Since at one time they were very close together, in the same general location, effectively contiguous. Ordinary expansion cosmology seems to be sufficient without inflation. (there is an inflationist answer to thus question which affirms that inflation WAS needed but let's understand the puzzle first.)

 

[rootone]

I think part of the confusion with the term 'singularity' arises from the usage of the term 'singular', to indicate a condition of an object (could be anything), which is very peculiar, unusual, unexpected, or hitherto thought to be impossible.
That is a legitimate usage of the word but is no longer commonly used, though it was quite popular in the earlier parts of the last century.
IIRC Conan Doyle's Sherlock Holmes detective character used 'singular' in that context a number of times when he had discovered mysterious evidence, but of course Holmes was not implying that he believed that the evidence was unphysical and had zero dimensions.

 

[JDoolin]

Last summer I subscribed to the International Astronomical Union long enough to download a whole bunch of CBET###.txt files from Harvard's database. This summer I've been trying to write up some perl scripts to pull the data out of each piece, getting the magnitude, the redshift, right-ascension, type and declination of each supernova in the list.

Here's a sample line: Supernova 2006sj, with it's discovery date, right ascension, declination, magnitude, redshift, and type
#2006sj# &Nov. 14& *2 10 22.418* ^- 3 33 09.32^ $23.0$ |0.7| ?Ia?

This is a pretty high redshift and high (dim) magnitude for a supernova in 2006. I'll have to get further into the data before I know whether by 2014 they were discovering much dimmer and more distant ones.

From what I've been led to understand, is that the nearby objects are receding at 74 km/s per MPc and the statistical fit is nearly perfect, and objects further away than about 6Gly are receding at less than 74 km/s per MPc, and there is a great deal of statistical "noise" beyond that point. Now whether this "noise" is due to actual differences, or measured differences, I don't know. Beyond 6 billion light years, you're getting into magnitudes well above (fainter) than 20, so the data might be difficult to get accurately.

Also, I'm not sure whether the redshift is calculated based on emission lines from the supernova itself, or the galaxy in which it is embedded. The issue of trying to use the supernova itself would be that it is light coming from exploding material that may be flying toward you at a significant speed. The issue of getting it from a galaxy is that the supernova might not actually be in that galaxy.

Also, I'm not sure what maximum brightness can be expected from the different types of supenova, (type Ia, Ib, Ic, II, etc). I think there would be a different magnitude-to-distance calculation for each type.

My impression, though, is that the best large-scale measurement of distance in cosmology is the magnitudes of these one-time explosions. In particular, the type I supernova which represent a very specific chain of events--matter accumulating on a white dwarf until it reaches a critical mass and converts into a neutron star.

The fact that we can see anything beyond 7 billion light years means that the big bang (everything starting from a point 13.7 billion years ago and moving outward at constant speed) cannot be right. But I usually find the explanations of "accelerating expansion" to be too vague in their relationship to the actual observed quantities.

 

[phinds]

The fact that we can see anything beyond 7 billion light years means that the big bang (everything starting from a point 13.7 billion years ago and moving outward at constant speed) cannot be right.

I don't follow your logic on that. What's special about 7 billion light years?

 

[JDoolin]

I don't follow your logic on that. What's special about 7 billion light years?

If the unmodified "Big Bang Theory" were correct, and everything in the universe came from a point 13.7 billion years ago and didn't accelerate, then the fastest it could be moving away is the speed of light, and the fastest it could return is the speed of light. So the furthest we could actually see is 13.7/2 = 6.85 billion light years.

6.85 billion years for the object to get to where we see it, and 6.85 billion years for the light to get to us.

 

[Bandersnatch]

Last summer I subscribed to the International Astronomical Union long enough to download a whole bunch of CBET###.txt files from Harvard's database. This summer I've been trying to write up some perl scripts to pull the data out of each piece, getting the magnitude, the redshift, right-ascension, type and declination of each supernova in the list.

Here's a sample line: Supernova 2006sj, with it's discovery date, right ascension, declination, magnitude, redshift, and type
#2006sj# &Nov. 14& *2 10 22.418* ^- 3 33 09.32^ $23.0$ |0.7| ?Ia?

You know, you can do such queries from publicly-available databases. Like Simbad:
http://simbad.u-strasbg.fr/simbad/sim-fid
e.g. use 'SN 2006' to display all supernovae in 2006; you may want to adjust output options first.
Here's a sample:

Spoiler

It's easy to find what you need there.

The issue of trying to use the supernova itself would be that it is light coming from exploding material that may be flying toward you at a significant speed.

That's not an issue. A light curve from any standard candle supernova looks the same - all such supernovae have the same proportion of material coming directly at you and traveling perpendicular to your line of sight, with the same associated broadening of the spectral lines. You then get this standard light curve and measure the redshift of the whole thing.

Also, I'm not sure what maximum brightness can be expected from the different types of supenova, (type Ia, Ib, Ic, II, etc). I think there would be a different magnitude-to-distance calculation for each type.

Supernovae of other types than Ia are not used as standard candles, since their light curves vary depending on progenitor star mass and composition. There's nothing standard about those, unlike Ia.

The fact that we can see anything beyond 7 billion light years means that the big bang (everything starting from a point 13.7 billion years ago and moving outward at constant speed) cannot be right. But I usually find the explanations of "accelerating expansion" to be too vague in their relationship to the actual observed quantities.

If the unmodified "Big Bang Theory" were correct, and everything in the universe came from a point 13.7 billion years ago and didn't accelerate, then the fastest it could be moving away is the speed of light, and the fastest it could return is the speed of light. So the furthest we could actually see is 13.7/2 = 6.85 billion light years.

6.85 billion years for the object to get to where we see it, and 6.85 billion years for the light to get to us.

It's true that 'everything starting from a point' cannot be right. But that is not what the Big Bang theory is! That's just a common misconception. The material you see at 6Gly did not need to 'go there' at the speed of light before sending you its signal.
What have you read so far about the theory? We could link you some reading material, but I don't want to send you stuff that's below your level.

 

[phinds]

If the unmodified "Big Bang Theory" were correct, and everything in the universe came from a point 13.7 billion years ago and didn't accelerate, then the fastest it could be moving away is the speed of light, and the fastest it could return is the speed of light. So the furthest we could actually see is 13.7/2 = 6.85 billion light years.

6.85 billion years for the object to get to where we see it, and 6.85 billion years for the light to get to us.

Ah. Got it. Thanks.

 

[marcus]

Bandersnatch post #40, right before this brief one of Phinds, is really informative over a wide range of issues including the standard candle SNe data base which is online and publicly available. Also at the end Bander has a response to JDoolin's idea about "6.85 billion years for the object to get there" that Phinds quoted just now. It's concise and potentially enlightening:
==quote Bander==
It's true that 'everything starting from a point' cannot be right. But that is not what the Big Bang theory is! That's just a common misconception. The material you see at 6Gly did not need to 'go there' at the speed of light before sending you its signal.
What have you read so far about the theory? We could link you some reading material, but I don't want to send you stuff that's below your level.
==endquote==
don't want to lose sight of that merely because we turned a page just now.

 

[JDoolin]

That Simbad thing is cool.

I was looking here at http://www.cbat.eps.harvard.edu/lists/RecentSupernovae.html about a year ago, and sent an email to somebody in charge there asking where I could access the redshifts. He said "in the individual CBETs". So I started downloading all the CBET's. Might have the same information as Simbad. But the CBET's do have more information... What kind of telescope; multiple observations of the supernova over time, magnitudes through different colored filters.

A light curve from any standard candle supernova looks the same - all such supernovae have the same proportion of material coming directly at you and traveling perpendicular to your line of sight, with the same associated broadening of the spectral lines. You then get this standard light curve and measure the redshift of the whole thing.

Thanks for that. I was momentarily under the impression that redshift couldn't be determined directly from the light of the supernova itself. But I see I was mistaken.

Here: https://en.wikipedia.org/wiki/Type_Ia_supernova#/media/File:SN1998aq_max_spectra.svg is the spectrum of a Type 1a supernova (taken in 1998). We could (perhaps) identify this pattern by the double-peak in the spectrum around 4000 angstroms. (Do you see the double-peak I'm talking about?)

So if that supernova happens something like a billion light years away, with a redshift of 0.7, then the double-peak would happen at somewhere around 4000*1.7=6800 angstroms. You would identify the redshift of 0.7 by the fact that the double-peak was around 6800 angstroms and solving the equation (1+z)4000=6800. Right?

Then by determining how "bright" the double-peak was--that is, what the intensity of the light through a spectrometer in the region of the double-peak, you would determine the magnitude of the supernova, right?

Now, how standard is this methodology for reporting supernova data, though? Does every astronomer reporting their data use compatible methodology so that everybody is measuring redshift and magnitude of the same features, and on the same scale?

 

[JDoolin]

I think it is an interesting thing to note, what Valenmur calls "constant expansion" is in some ways exponential.
After one period of time the distance from green to blue doubles. After another equal period, that distance doubles again.

The same can be said for the distance from green to purple, and for the distance from green to red.

Is that a standard description of what is meant by constant expansion?

I would probably represent that as dr/dt = k r.
dr/r = k dt
ln r = k t
r = e ^(kt)

r = r_0 * 2^t

 

[Bandersnatch]

But the CBET's do have more information... What kind of telescope; multiple observations of the supernova over time, magnitudes through different colored filters.

I'm pretty sure all those data are accessible from Simbad or the other interfaces listed in the top toolbar on that site. Have a look through the 'output options' and/or display detailed view of an object and explore the links therein.
But perhaps it's easier for you to pull data from your files - I wouldn't know. Just mentioning that there are other options.
By the way, this catalogue:
http://cds.aanda.org/component/article?access=bibcode&bibcode=2012A%2526A...538A.120L
combines CBAT and two others, with some refinement. It's also viewable from Simbad and VizieR on the CDA site. The paper has some links and good discussion of the parameters used - it might be of interest to you.

Here: https://en.wikipedia.org/wiki/Type_Ia_supernova#/media/File:SN1998aq_max_spectra.svg is the spectrum of a Type 1a supernova (taken in 1998). We could (perhaps) identify this pattern by the double-peak in the spectrum around 4000 angstroms. (Do you see the double-peak I'm talking about?)

So if that supernova happens something like a billion light years away, with a redshift of 0.7, then the double-peak would happen at somewhere around 4000*1.7=6800 angstroms. You would identify the redshift of 0.7 by the fact that the double-peak was around 6800 angstroms and solving the equation (1+z)4000=6800. Right?

That's pretty much it, as far as I understand it. You can do a similar analysis with black body spectrum of the CMBR, by the way.
The only issue in what you wrote is tangential to the question: z=0.7 corresponds to about 5 Gly at the time of emission, and about 8.5 Gly now, not 1 Gly.

Then by determining how "bright" the double-peak was--that is, what the intensity of the light through a spectrometer in the region of the double-peak, you would determine the magnitude of the supernova, right?

If you mean apparent magnitude in that band, then yes, it would do. Absolute magnitude ordinarily needs knowledge of distance to calculate. For SN Ia absolute magnitude is always the same (in the sense of e.g. peak magnitude; of course it varies in time for each explosion, but in the same way).

Now, how standard is this methodology for reporting supernova data, though? Does every astronomer reporting their data use compatible methodology so that everybody is measuring redshift and magnitude of the same features, and on the same scale?

I can't help you here. Those are the basics behind the observations. What a typical observation and analysis consists of I do not know, but I'd imagine them to be pretty standardized, considering for how long they've been made.
For something more informative on methodology you'd need to ask somebody who actually does this for a living. Or, what you could do is follow the bibliography Simbad lists for each object and check the methodology in those papers. If it's at all listed, that is. It might be considered trivial.

I think it is an interesting thing to note, what Valenmur calls "constant expansion" is in some ways exponential.
After one period of time the distance from green to blue doubles. After another equal period, that distance doubles again.

The same can be said for the distance from green to purple, and for the distance from green to red.

Is that a standard description of what is meant by constant expansion?

Yes. It means that the first derivative of the scale factor is constant.
By analogy, this is the same as saying that your savings account is growing at constant rate of X% of compound interest, even as the actual amount of money grows exponentially.
Similarly, accelerated expansion means that the first derivative of a(t) increases over time. These are the meanings of acceleration/constancy/deceleration of expansion used in cosmology - not the change in velocities of individual galaxies.
By focusing on a single point in Valenmur's graphs and its motion with respect to the origin over the history of expansion, you may observe accelerated motion even as the expansion is decelerating.

 

[JDoolin]

This is a question for clarification and verification. Valenmur presented three different models

(1) If we had the "constant expansion" universe, the governing differential equation would be \frac{dr}{dt}=a(t) r, and a(t) is constant in time. It simplifies to \frac{dr}{dt}=k r

(3) If we were to describe that model where everything in the universe starts at a point, and moves outward from that point at constant speed, then the equation for that would be distance = velocity * time or in differential form: \frac{dr}{dt}=\frac{r}{t}. This is what shows up in valenmur's diagram as a "decelerating expansion". Or to use the \frac{dr}{dt}=a(t) r description, you could define a scale factor a(t)\equiv \frac{1}{t}.

(3) If we have an "accelerating expansion" universe, the governing differential equation would be the same, (\frac{dr}{dt}=a(t) r), but a(t) would be increasing over time. For instance, one example might be \frac{dr}{dt}=k t rI am surprised by this, because I would have thought of (2) as being "constant expansion" whereas (1) is exponentially increasing expansion, and (3) is, perhaps "hyperexponential" expansion.

 

[Egregious]

I have a very brief layman's question. Thank you everyone for the lively discussion that is mostly over my head.

Q) Based on red-shift, do we know/speculate/theorize that the acceleration of the universe is increasing or decreasing?

There are more technical ways to ask this question. Note that I do understand the difference between acceleration and deceleration. That is not my question. I want to know if there is a contemporary belief about the changing nature of the acceleration of the expanding universe over time. (i.e.: What is happening to the rate of acceleration?) Feel free to be blunt in your replies - I can take it. e.g. I realize that it may be well beyond our collective capacity to measure this with precision over the course of time that we have observed the red shift phenomenon. I have no idea whether this question asks the impossible, or not. I have been wondering this for a while, and unfortunately, the keywords are too common for me to locate an answer.

Thank you kindly.

 

[marcus]

It could help to be clearer what the expansion history looks like and what the acceleration looks like, and think about how you'd assign an amount to it. How you'd quantify it so you could gauge how it was increasing.
In this graph the blue curve shows the size of a generic distance. 0.8 is the present moment in time.
The curve tracks a distance which is set to ONE at the present. For example it could be a distance that is one billion light years at present---and we can look back and see its past history as it grew. And its projected growth in the future.

Think of the the scale on the horizontal axis measuring time in units of 17.3 billion years.
The changeover from deceleration to acceleration happened between time 0.4 and 0.5 when the distance was about level 0.6 on the vertical scale. When it was about 60% of its present-day size.
The deceleration (until around time 0.44 or 0.45) is fairly subtle but we can still see it by eye, in the curve of distance growth. The acceleration is very gentle at first, barely visible. But it gradually builds up.

I'll pause here in case you want to think about this, ask questions. Maybe other people want to respond too, or will explain more stuff. How the model is fitted to observational data. How the model is based on our best theory of the way gravity works: General Relativity as written down in 1917. The equation underlying the curve is derived from the GR equation. GR has been challenged and tested many ways over the years and is supported by a a large amount of data. The standard cosmic model is derived from GR and is in its turn the best fit to a large amount of astronomical data. It does not require the existence of any mysterious "dark energy" , it simply posits a cosmological curvature constant Lambda which governs the longterm fractional growth rate of distance which is expected to level out at around 1/173 of one percent per million years. (The fractional growth rate of distance is the gold curve in the picture, you can see it has been declining and has started to level off.) "Dark energy" was made up as one speculative way to explain Lambda but so far there is no evidence that the curvature constant is anything but that, a constant curvature. Other people may want to discuss this. My main aim here is just to show the expansion history curve and point out the slight deceleration and acceleration in it, to give an idea of what we are actually talking about.

 

[Egregious]

It could help to be clearer what the expansion history looks like and what the acceleration looks like, and think about how you'd assign an amount to it. How you'd quantify it so you could gauge how it was increasing.

I believe that this was in response to my inquiry. Thank you, Marcus for your kind reply and for everything you do for this community.

Again, I am not a physicist. I am merely attempting to resolve a logical conflict in my own mind. Briefly, I agree that a richer understanding of expansion history, but I do not have the requisite tools to begin to understand what happened early in the history of the universe with inflation theory and such (I am 44 years old at the onset of my own quest of self-learning). I do have a cursory understanding of red-shift and the the expanding universe idea. Specifically, images used by Professor Krauss and others have fostered my understanding of the present expansion and why there is no 'center' of the universe. I get this:

https://s16-us2.ixquick.com/cgi-bin/serveimage?url=http%3A%2F%2Fts2.mm.bing.net%2Fth%3Fid%3DJN.GTToVI6o%252fk6J4ZSftGq3bw%26pid%3D15.1%26f%3D1&sp=e79792a08764088e95042fb134e03448​

The logical problem I am confronting goes like so:

1. Nothing can travel faster than the speed of light.
2. Every celestial body is moving away from my planet [i.e. relative to me; i.e the universe is expanding (with a few anomalous exceptions)].
3. This expansion is accelerating.

[edited to merge identical concepts]

My question is whether #3 is also increasing. If I understand your diagram correctly, this appears to be the case (I need to revisit my calculus education). If so, or even if the acceleration is constant, wouldn't there be a a time that #1 is violated relative to earth. This is troubling.

I realize that there may be many esoteric details that I am not prepared to understand. I am embarking on my learning journey from the starting point now to hopefully one day understand more complex questions such as my immediate inquiry. Again, kindly feel free to be blunt: "You are not there yet" is a perfectly acceptable response.

Many kind thanks and warmest regards.

 

[Bandersnatch]

If so, or even if the acceleration is constant, wouldn't there be a a time that #1 is violated relative to earth. This is troubling.

See this FAQ entry:
https://www.physicsforums.com/threads/at-what-velocity-does-the-universe-expand-can-it-be-faster-than-light.508610/