THE HARLEQUIN
- 52
- 4
two spacecraft s travel parallel to each other along straight lines AB and CD as shown in the picture here ...
while s1 moves with a simple harmonic motion , s2 moves with a constant speed and only at points A and B it gets enough thrust within a very negligible time to reverse its direction of velocity ...
s1 and s2 travel the same AB=CD distance after a same amount of time ..
now both of the spacecraft s fire rockets R1 and R2 at the same time from points D and B respectively and they come back after time t .
now if S1,R1, S2,R2 carry 4 persons of the same age then after time t when they meet
1. what will be the difference between their ages ?
2. on what condition it is possible for all of them to have the same age when they meet ?
[ note: you can take v of S2 and f of S1 arbitrarily ]
answers with proper visualizing power will be appreciated ... mathematical analysis is also appreciated but not needed ...
THE HARLEQUIN
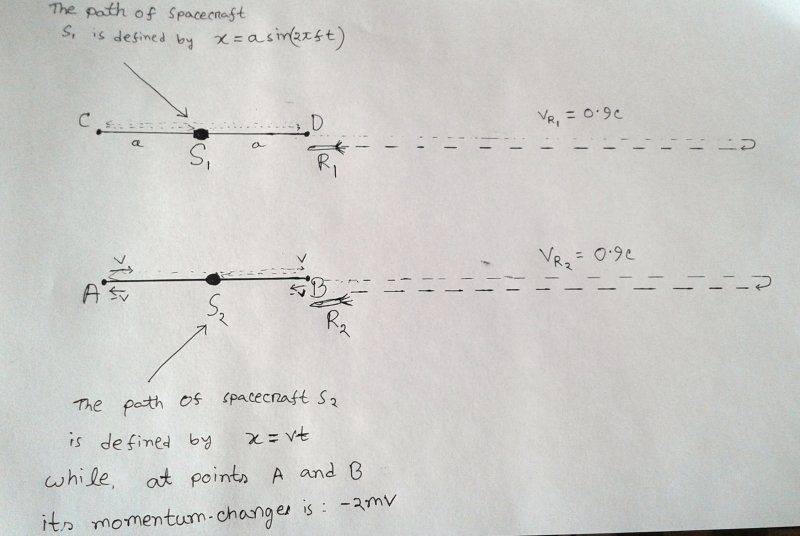
while s1 moves with a simple harmonic motion , s2 moves with a constant speed and only at points A and B it gets enough thrust within a very negligible time to reverse its direction of velocity ...
s1 and s2 travel the same AB=CD distance after a same amount of time ..
now both of the spacecraft s fire rockets R1 and R2 at the same time from points D and B respectively and they come back after time t .
now if S1,R1, S2,R2 carry 4 persons of the same age then after time t when they meet
1. what will be the difference between their ages ?
2. on what condition it is possible for all of them to have the same age when they meet ?
[ note: you can take v of S2 and f of S1 arbitrarily ]
answers with proper visualizing power will be appreciated ... mathematical analysis is also appreciated but not needed ...
THE HARLEQUIN
Last edited: