A quadrilateral inscribed in a semicircle

[anemone]

Let $PQRS$ be a quadrilateral inscribed in a semicircle with diameter $PS=x$. If $PQ=a$, $QR=b$, $RS=c$, then prove that $x^3-(a^2+b^2+c^2)x-2abc=0$.

 

[Opalg]

[sp]

View attachment 1706​

Denote the angles at $O$ as $2\alpha$, $2\beta$, $2\gamma$, as in the diagram. Note that $\sin\alpha = \dfrac{a/2}{x/2} = \dfrac ax$, and similarly $\sin\beta = \dfrac bx$, $\sin\gamma = \dfrac cx.$ Also, $\alpha + \beta + \gamma = \pi/2$, so that $\sin\alpha = \cos(\beta + \gamma) = \cos\beta\cos\gamma - \sin\beta \sin\gamma$. Hence $\cos\beta\cos\gamma = \sin\alpha +\sin\beta \sin\gamma$, and similarly $\cos\alpha\cos\gamma = \sin\beta +\sin\alpha \sin\gamma$. Then $$\begin{aligned}1 = \sin(\alpha+\beta+\gamma) &= \sin(\alpha+\beta)\cos\gamma + \cos(\alpha+\beta)\sin\gamma \\ &= \sin\alpha\cos\beta\cos\gamma + \cos\alpha\sin\beta\cos\gamma + \sin^2\gamma \\ &= \sin\alpha(\sin\alpha + \sin\beta\sin\gamma) + \sin\beta(\sin\beta + \sin\alpha\sin\gamma) + \sin^2\gamma \\ &= \sin^2\alpha + \sin^2\beta + \sin^2\gamma + 2\sin\alpha\sin\beta\sin\gamma. \end{aligned}$$ Now all you have to do is to substitute the values $\sin\alpha = \dfrac ax$, $\sin\beta = \dfrac bx$, $\sin\gamma = \dfrac cx$ to get $1 = \dfrac{a^2}{x^2} + \dfrac{b^2}{x^2} + \dfrac{c^2}{x^2} + 2\dfrac{abc}{x^3}$, from which $x^3 = (a^2 + b^2 + c^2)x + 2abc.$[/sp]

 

[anemone]

[sp]

View attachment 1706​

Denote the angles at $O$ as $2\alpha$, $2\beta$, $2\gamma$, as in the diagram. Note that $\sin\alpha = \dfrac{a/2}{x/2} = \dfrac ax$, and similarly $\sin\beta = \dfrac bx$, $\sin\gamma = \dfrac cx.$ Also, $\alpha + \beta + \gamma = \pi/2$, so that $\sin\alpha = \cos(\beta + \gamma) = \cos\beta\cos\gamma - \sin\beta \sin\gamma$. Hence $\cos\beta\cos\gamma = \sin\alpha +\sin\beta \sin\gamma$, and similarly $\cos\alpha\cos\gamma = \sin\beta +\sin\alpha \sin\gamma$. Then $$\begin{aligned}1 = \sin(\alpha+\beta+\gamma) &= \sin(\alpha+\beta)\cos\gamma + \cos(\alpha+\beta)\sin\gamma \\ &= \sin\alpha\cos\beta\cos\gamma + \cos\alpha\sin\beta\cos\gamma + \sin^2\gamma \\ &= \sin\alpha(\sin\alpha + \sin\beta\sin\gamma) + \sin\beta(\sin\beta + \sin\alpha\sin\gamma) + \sin^2\gamma \\ &= \sin^2\alpha + \sin^2\beta + \sin^2\gamma + 2\sin\alpha\sin\beta\sin\gamma. \end{aligned}$$ Now all you have to do is to substitute the values $\sin\alpha = \dfrac ax$, $\sin\beta = \dfrac bx$, $\sin\gamma = \dfrac cx$ to get $1 = \dfrac{a^2}{x^2} + \dfrac{b^2}{x^2} + \dfrac{c^2}{x^2} + 2\dfrac{abc}{x^3}$, from which $x^3 = (a^2 + b^2 + c^2)x + 2abc.$[/sp]

Thank you Opalg for participating!

My solution:

Spoiler

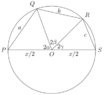
From the Ptolemy Theorem, we have the product of diagonals equals the sum of the products of the opposite sides for any cyclic quadrilateral.

View attachment 1752
So, in our case, we have the following identity from the Ptolemy Theorem:

$PR \cdot QS=ac+bx$---(1)

In order to get rid of the variables $PR$ and $QS$, we have to relate them to the variables $a, b, c, x$ and this can be done by observing there are two right-angle triangles exist in the diagram since PS is the diameter of the cicle, so by applying the Pythagoras' Theorem to each of these triangles we get:

$PR^2=x^2-c^2$ and $QS^2=x^2-a^2$

Hence, raise the equation (1) to the second power and replace the two equations above into it gives

$PR^2 \cdot QS^2=a^2c^2+b^2x^2+2abcx$

$(x^2-c^2)(x^2-a^2)=a^2c^2+b^2x^2+2abcx$

$x^4-a^2x^2-c^2x^2+\cancel{a^2c^2}=\cancel{a^2c^2}+b^2x^2+2abcx$

$x^4-a^2x^2-c^2x^2=b^2x^2+2abcx$

$x^4-(a^2+b^2+c^2)x^2-2abcx=0$

$\therefore x^3-(a^2+b^2+c^2)x-2abc=0$ since $x\ne 0$ and we're done.