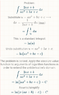A query in integration using method of substitution

[Wrichik Basu]

Homework Statement

:[/B]

I was learning the use of standard forms in method of substitution in solving integration. My book has given this method for solving integrals of the type $\int \frac{lx +m}{ax^2+bx+c} dx$:

As an example, the book gives this one:

Homework Equations

:[/B]

The Attempt at a Solution

How does one solve to get the circled part? I can understand that the book is separating the two parts of the numerator. I also know how to solve the second part, but how does one reach the circled part?

 

[Arman777]

For $k_1\int \frac {2ax+b} {ax^2+bx+c}\, dx$ you need another substitution.

 

[Wrichik Basu]

For $k_1\int \frac {2ax+b} {ax^2+bx+c}\, dx$ you need another substitution.

Even I was thinking that. How do I solve that part: $k_1 \int \frac{2ax +b}{ax^2+bx+c} dx$? As per the book, I do not require another substitution. So, how should I proceed with that part?

 

[Wrichik Basu]

Searching the Internet for something called an "integral calculator", I found one, and it showed me the steps properly:

This solves my problem. The book had done it in one step, which is why I was facing the problem.

 

[Arman777]

It's nice but it would be better If you work by yourself and find the solution. Anyways yes, that's how you do it.

 

[Ray Vickson]

Searching the Internet for something called an "integral calculator", I found one, and it showed me the steps properly:

View attachment 221031

This solves my problem. The book had done it in one step, which is why I was facing the problem.

When you are a beginner, just starting to learn the subject, you should avoid such on-line tools (except, possibly to check your work). You will never figure out how to do integrals without doing lots of examples by hand and without assistance from computer-aided integration tools. Think of it this way: what would you do on an exam, where you have no access to such facilities?

 

[Wrichik Basu]

When you are a beginner, just starting to learn the subject, you should avoid such on-line tools (except, possibly to check your work). You will never figure out how to do integrals without doing lots of examples by hand and without assistance from computer-aided integration tools. Think of it this way: what would you do on an exam, where you have no access to such facilities?

I solve problems from at least two books before proceeding to a new topic. Help materials like online calculators help in self study and nothing else, especially when you're stuck at a problem you just can't solve.

 

[epenguin]

The expression to be integrated is a linear function divided by quadratic. A linear function is the derivative of a quadratic. So if you were lucky the numerator would be the derivative of the denominator, i.e. the expression to be integrated wrt x would be $\dfrac {f'\left( x\right) }{f\left( x\right) }$ which I presume you know how to do. In this case we are as usual not so lucky, but we can make it into a linear part which is part which is derivative of the denominator (just hammering the constants) with some other constant leftover – that second part then being a constant divided by a quadratic which we know how to integrate. Well actually many people would think that second part is the most difficult one.