A question about conditions for Weightlessness

[nadavg54]

I read that if you are in a spaceship orbiting Earth in a circular motion, the astronout feels weightless (meaning the normal force to the astronout is equal to zero). But according to Newton laws equations you get:

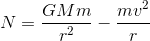
and then if we assume N=0 (which is really what's happening according to my understanding), we get:

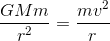
And I don't understand why is that true, if you can explain, or if there is any mistake in what I've said above,

Thanks

 

[Doc Al]

The only force acting on the ship is gravity, which is just enough to keep it in orbit. No additional force is required to support something in orbit, so the apparent weight is zero.

 

[russ_watters]

In orbit, the force of gravity isn't felt because the orbiting spaceship is in freefall.

 

[nadavg54]

so my equations are not correct?

 

[willem2]

so my equations are not correct?

They are correct. N=0 for an astronaut in freefall, because there's nothing that
can push against the astronaut. Your equation is just F =ma , where the
force is \frac {GmM}{r^2} and the acceleration is <br /> \frac {v^2}{r}

 

[chrisbaird]

Yes, your equations are correct. We actually don't "feel" gravity, we feel the ground pushing on our feet on response to the gravity pulling us against the ground. In free fall, there is no ground pushing back, so we feel don't feel it. But there is still gravity pulling on us. That is why we accelerate downwards. Try jumping off a high bridge into a river with your eyes closed. While in the air, you will feel weightless, but gravity is still at work, because you fall.