A question about Faraday's law

[LiorE]

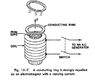
My question is about the system in the picture. There is an upwards force which acts on the ring. My problem is that I don't see how it comes about. I mean, suppose that at time t, the current through the coil flows counterclockwise and is increasing. So there is an increasing, upward pointing magnetic field through the ring. That should induce a current on it in a clockwise direction. But then, according to the Lorentz force equation, the force on the ring should be sideways, isn't it? I mean it dosen't make sense that the force will be in the same direction as the magnetic field anyway, because \vec F = q(\vec{v} \times \vec{B}), so it has to be perpendicular to both v and B.

So how is that force created?

Thanks in advance,

Lior

 

[ibc]

This should give you an idea:
http://img253.imageshack.us/img253/3589/76749370cc6.png

(sorry for the ugly sketch, any reference to a sketch making program would be appreciated =x )

 

[LiorE]

Oh, I get it - because B has a component parallel to the ring. Thanks!

 

[granpa]

k3d
"google sketchup"

 

[Phrak]

Oh, I get it - because B has a component parallel to the ring. Thanks!

No... B has a components perpendicular to the ring. In the region of the ring, B has both radial and axial components.

 

[Phrak]

This is actually a very interesting question, guys.

With an infinitely long core, the B field will be purely axial, following along the core. the Lorenz force on the charges moving in the ring are anti-radial--directed inward. So is the ring repelled in this case?? I don't think so. There's no preferred axial direction. But at the end of the core, or the end of a solenoid, the field diverges outward, radially. This would seem to be the cause for the ring being repelled.

Remember, this only works for an AC current in the coil. From what I can deduce, the changing flux passing through the ring induces a circumpherential electric field inducing a current in the loop. But the radial component of the magnetic field in the region of the ring acts under the Lorentz force,

F_z = q v_phi B_r

to push the ring away.

Any Yays, or Nays, your just another lunatic on the internet?