A question about improper integrals

[saltydog]

The following is an outgrowth from a problem I encountered in the Homework section concerning the convergence of:

\int_0^{\pi/2} ln[sin(x)]dx

I feel there is some way of separating the region around an asymptote, say x=b, into a region which yields a convergent integral and a region which does not. My initial suspicions is that the boundary is marked by the functions:

g1(x)=\frac{1}{x-b}\quad\text{and}\quad g2(x)=\frac{1}{b-x}

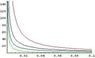
This is shown in red in the attached plot along with functions in blue which have a convergent improper integral and one in green which does not.

I'm considering the following proposition:

Let f(x) be bounded on the interval [a,b) with:

\mathop\lim\limits_{x\to b} f(x)=\infty

Then:

\int_a^b f(x)dx

converges iff the following is true:

\exists x_c \in [a,b) : |f(x)|<\frac{1}{|x-b|} \quad\forall x\in [x_c,b)

That is, if f(x) ever strays onto or outside the region bounded by g1 and g2 and remains there as x goes to b, then the integral will necessarilly diverge. If it remains interior to the region, it converges.

My initial thoughs are the integrals:

\int_0^1 \frac{1}{x^k}dx

which converge if k<1 and diverge otherwise.

Can such a general statement by made for functions in general no matter how complex?

I'll attempt to prove it false by finding a counter-example but I've found none so far.

What do you guys think?

 

[mathman]

For x near 0, sin(x) is approx. x. The integral of ln(x) diverges as x ->0, therefore so does the integral of ln(sin(x)).

 

[saltydog]

For x near 0, sin(x) is approx. x. The integral of ln(x) diverges as x ->0, therefore so does the integral of ln(sin(x)).

Hello Mathman. Perhaps I'm missing something. My understanding is:

\int_0^{\pi/2} ln[Sin(x)]dx=-\frac{\pi}{2}ln(2)

 

[lurflurf]

Let f(x) be bounded on the interval [a,b) with:

\mathop\lim\limits_{x\to b} f(x)=\infty

I think you mean
Let f(x) be bounded on the interval [a,c] for any c in [a,b)
Clearly f(b-)=infinity implies f is not bounded on [a,b)

Sometimes it helps to think of impropper integrals of types one and two as being almost the same thing in different cordinates
let u=log(x)
\int_0^h \log(x) dx=\int_{-\infty}^{log(h)} u e^u du=-h+h\log(h)
so these diverge or converge together

 

[saltydog]

I think you mean
Let f(x) be bounded on the interval [a,c] for any c in [a,b)
Clearly f(b-)=infinity implies f is not bounded on [a,b)

Yes Lurflurf, my mediocrity in Analysis shines through. I make no bones about it. Thanks for clearing that up for me. You know, I may not be gifted in Analysis but I am a bit persistent.

What about the general suitability of the proposition? Rubbish or noteworthy? I shall continue to investigate it unless a counter-example is found.

 

[lurflurf]

consider f(x)=1/(2x-2b)
f(x)<1/(x-b)
but diverges
you need
f(x)<1(x-b)^(1+epsilon)
for some positive epsilon
once you do you will have a result that is a special case of the comparison test
x^(1-epsilon) converges on (0,1) if epsilon is positive thus any thing smaller than it will converge.

 

[saltydog]

consider f(x)=1/(2x-2b)
f(x)<1/(x-b)
but diverges
you need
f(x)<1(x-b)^(1+epsilon)
for some positive epsilon
once you do you will have a result that is a special case of the comparison test
x^(1+epsilon) converges on (0,1) if epsilon is positive thus any thing smaller than it will converge.

Alright. I understand the counter-example but it's not clear at all to me about the:

f(x)&lt;\frac{1}{(x-b)^{1+\epsilon}}

Also the part:

x^(1+epsilon) converges on (0,1) if epsilon is positive thus any thing smaller than it will converge.

Is that a typo? I mean that converges even if epsilon is zero.

I'll spend some time with this. It's interesting for me and thanks for helping me.

 

[shmoe]

Multiplying by 1/2 is an unsubtle way of breaking this boundary, you might try to patch your conjecture by allowing for a constant times your "boundary function", like a big-O order of growth condition. This will fail also. 0&lt;\frac{-1}{x(-\log{x})}&lt;\frac{1}{x} on (0,0.5), but it's integral diverges here. You can keep finding functions of smaller and smaller order like this with divergent integrals in an appropriate interval around zero by adding more log's (and appropriate absolute value signs).

On the other hand the integral of \frac{1}{x(-\log{x})^{1+\epsilon}} on (0,0.5) will converge for any epsilon>0. Yet \frac{1}{x^{1-\delta}}&lt;\frac{1}{x(-\log{x})^{1+\epsilon}} for any delta>0 when x is close enough to 0. There's no clear boundary either way.

 

[saltydog]

Multiplying by 1/2 is an unsubtle way of breaking this boundary, you might try to patch your conjecture by allowing for a constant times your "boundary function", like a big-O order of growth condition. This will fail also. 0&lt;\frac{-1}{x(-\log{x})}&lt;\frac{1}{x} on (0,0.5), but it's integral diverges here. You can keep finding functions of smaller and smaller order like this with divergent integrals in an appropriate interval around zero by adding more log's (and appropriate absolute value signs).

On the other hand the integral of \frac{1}{x(-\log{x})^{1+\epsilon}} on (0,0.5) will converge for any epsilon>0. Yet \frac{1}{x^{1-\delta}}&lt;\frac{1}{x(-\log{x})^{1+\epsilon}} for any delta>0 when x is close enough to 0. There's no clear boundary either way.

Thanks Shmoe. I'll work with it. My motivation for such is simple:

I simply wish to learn what is the defining characteristic of a function near it's asymptote which determines if the integral about same converges? Is there no way of "extracting" this defining characteristic (in general terms applicable to all functions)? An example scenario I imagine would be: "if the first derivative does this and the second and higher ones do this, than the integral converges".

 

[saltydog]

I wish to revise my conjecture above (I can do that right?). Perhaps "scrap it" would be more appropriate. The plot below is for the four functions:

\text{green:}\quad\frac{1}{10x}\quad<br /> \text{black:}\quad \frac{1}{x^{4/5}}\quad<br /> \text{blue:}\quad\frac{-1}{xln(x)}\quad<br /> \text{red:}\quad \frac{1}{x}


As is evident in the plot, all the other functions are inside 1/x yet only the improper integral of x^{-4/5} converges. Note also \frac{-1}{xln(x)} and 1/10x are inside the black curve yet the improper integrals of these two functions still diverge. However, close to the y-axis (at 10^-6), the black line crosses-over both of these functions and thus comes closer to the y-axis.

I don't know about you guys, but I look at this plot, it's telling me something yet I can't figure out what it is.

 

[lurflurf]

Alright. I understand the counter-example but it's not clear at all to me about the:

f(x)&lt;\frac{1}{(x-b)^{1+\epsilon}}

Also the part:



Is that a typo? I mean that converges even if epsilon is zero.

I'll spend some time with this. It's interesting for me and thanks for helping me.

\int_0^1 x^{-1+\epsilon} dx
converges when 0<epsilon
it diverges otherwise (in particular it diveges if epsilon=0)
It is a well know result that if
f(x) is continuous and bounded on [a,c] for all c in (a,b) and
\int_a^b f(x) dx
converges and g(x)<=f(x) (presuming for simplicity f,g>=0) then
\int_a^b g(x) dx
converges
the fact that some function is less than another that diverges gives no information
also it is tempting to believe that x^-1 is the border between convergent and divergent function, but it is not really true. There is a lot going on. Oh and throw 1/x^.9 onto your graph.

 

[lurflurf]

Alright. I understand the counter-example but it's not clear at all to me about the:

f(x)&lt;\frac{1}{(x-b)^{1+\epsilon}}

Also the part:



Is that a typo? I mean that converges even if epsilon is zero.

I'll spend some time with this. It's interesting for me and thanks for helping me.

yes should be 1-epsilon

 

[saltydog]

Well, I found two good sites on the web concerning convergence test for improper integrals. Yea, I should know these already, or forgot them or whatever. They are:

First link to convergence test

Second link to convergence test

What gets me, and I'm not trying to criticize anyone here cus' I'm in no position to do so, but what led me to all this was the Homework Forum question: does the following integral converge:

\int_0^{\pi/2} ln[Sin(x)]dx

Well, after reviewing the convergence tests above, it's just obvious it converges just by inspection. And I don't need any colored graphics neither. That is:

Sin(x)\approx x \quad\text{when}\quad x\approx 0

Thus:

ln[Sin(x)]\approx ln(x)\quad\text{when}\quad x\approx 0

And:

\int_0^a ln(x)dx=(xln(x)-x)\left|_0^a

Via L'Hopital's rule, that limit is aln(x)-a. Thus the integral converges, thus the one with Sin(x) converges too.

I'm still not satisfied though: I still feel there is some defining characteristic of functions which have convergent improper integrals about asymptoes that can be determined without using these tests or evaluating the antiderivative.

 

[mathman]

My apologies. I wasn't thinking straight. Saltydog got it right.