- #1
typhoonss821
- 14
- 1
hallow everyone
i am a tenth-grade student in Taiwan.What i want to know is that how to proove the curvature at point (a,(f(a))(assume f(x) is smooth at this point) is
f"(a)/(1+f'(a)^2)^(3/2))
i've thought this way:consider a circle first
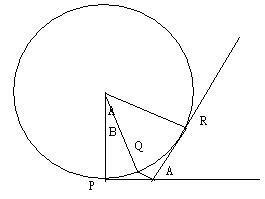
in this circle the curvature at point P is lim arcPR/A as R approaches P ,curvature at point Q supposesd to be lim arcQR/(A-B) as R approaches Q
it might be d(arcQR)/d(A-B),equaling to d(arcQR)/d(A-(A-B)),because (A-B) is constant,it also equals to arcPR/A
So if we draw an ossculating cirsle at (a,(f(a)) ,we can reply the conclusion to deal with the problem,is this saying right??
i am a tenth-grade student in Taiwan.What i want to know is that how to proove the curvature at point (a,(f(a))(assume f(x) is smooth at this point) is
f"(a)/(1+f'(a)^2)^(3/2))
i've thought this way:consider a circle first
in this circle the curvature at point P is lim arcPR/A as R approaches P ,curvature at point Q supposesd to be lim arcQR/(A-B) as R approaches Q
it might be d(arcQR)/d(A-B),equaling to d(arcQR)/d(A-(A-B)),because (A-B) is constant,it also equals to arcPR/A
So if we draw an ossculating cirsle at (a,(f(a)) ,we can reply the conclusion to deal with the problem,is this saying right??
Last edited: