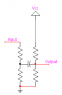Choosing a capacitor
In general for a sinusoidal signal, we would like the impedance of the capacitor to be as small as possible. In that case, it looks like we should just choose as big a capacitance as possible.
This is also true in theory, but the true practical capacitor is not just capacitance, it is actually modeled by the following:
Z_{c} = R_{c} + j\omega L + \frac{1}{j\omega C}
Yes that is true, the capacitor also has an inductance (although very small), and a resistance (very big).
However, you can see, that as the frequency increases and the term from the capacitance becomes smaller, but the term containing inductance gets larger. So for every capacitor, there is a frequency where, instead of the impedance getting smaller and smaller, it begins getting bigger and bigger. This is called the self-resonant frequency.
Now the inductance L depends on how the capacitor is built, but in general, the bigger capacitor, the bigger inductance it will have. So higher capacitance will give you a higher inductance, which in turn will mean a lower self-resonant frequency.
So in conclusion, when choosing the capacitor you would of course look at the frequency or frequencies it's going to work with, and then try to choose a high capacitance, but small enough so that the operating frequency is still lower than the self-resonant frequency.
How to do this? Look at the datasheet for the capacitor, it will have a graph of the impedance versus frequency, and there you can see the self resonant frequency.
But for starters: Just choose a high capacitance, since you most likely won't be using a high enough frequency (it is more in RF systems this has to be taken into account).
The square wave
Have you learned about Fourier Series? If you have, then you can decompose the square wave signal into a sum of normal sinusoids.
v_{sq} = a_{0} + \sum{a_{n}cos(n\omega_{0} t)} + \sum{b_{n}sin(n\omega_{0} t})
The sums are from 0 to ∞.
Now ω0 is the fundamental frequency and is the frequency of the periodic signal you are trying to model (the square wave).
a0 is the DC term. It is actually the frequencies where n = 0 (frequency 0).
What happens in the circuit
Now if the square wave signal is represented by all these different sinusoids, we can just apply superposition and and look at what happens for each and every one of them.
As you can see, all frequencies other than the fundamental one are greater than the fundamental frequency (because n is a positive integer). Only the DC term has a "lower" frequency (It's 0).
So if we have chosen the capacitance so that the fundamental frequency gives a small enough impedance, all other frequencies will have an even smaller impedance.
The DC term however, will have frequency 0, which means the impedance will be infinite.
The transient versus steady-state response
The impedance model of a circuit tells us about the steady-state response of the system. That is, how the voltages and currents will look after some time has gone by. What goes on before this is called the transient response.
You can find out the transient response by using LaPlace transforms and solving differential equations.
So what is the conclusion?
Well, since the DC term at steady state will meet an infinite impedance, it won't be visible at at the node left of the middle capacitor. However, all the other frequencies should be let through quite nicely. Here is a circuit that shows how it look: I have chosen the same values as you did, and I am probing the following places:
Blue: voltage of the signal generator
Green: voltage at left side of C1
Red: voltage at right side of C1
As you can see, after approximately 40ms, the "transient response" has died out, and we are left with the steady state response.
If you want to know more, you should really study Fourier Series and Fourier transforms and Laplace Transforms and possibly Control theory. These things will give you several ways of understanding a system like this.
EDIT: Attached the image ;)