rover_dude
- 18
- 0
Homework Statement
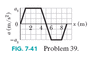
Figure 7-39 (attached) gives the acceleration of a 3.0 kg particle as an applied force moves it from rest along an x-axis from x = 0 to x = 9.0 m. The scale of the figure's vertical axis is set by as = 8.0 m/s2. How much work has the force done on the particle when the particle reaches (a)x = 4.0 m, (b)x = 7.0 m, and (c)x = 9.0 m? What is the particle's speed and direction (give positive answer if the particle moves along x-axis in positive direction and negative otherwise) of travel when it reaches (d)x = 4.0 m, (e)x = 7.0 m, and (f)x = 9.0 m?
Homework Equations
Equations I used: Area of a right triangle (1/2)(a)(b) where a and b are legs and NOT the hypotenuse. Area of a rectangle l*w (length times width) W=Kf-Ki (since Ki is 0) W=(1/2)mv^2 v=sqrt((2W)/m))
The Attempt at a Solution
Okay, this is online homework and I tried 3 different times and got the same answers, but it says they are wrong I have no idea why. So here it goes.for (a) I took the area from 0-4 of what is under the lines, so I got (1/2)(1)(8)+(3*8) to get 28. for (b) Same thing: 2(1/2)(1)(8)+(3*8)-(1/2)(1)(8)-(1)8 to get 20 (c) 2(1/2)(1)(8)+(3*8)-2(1/2)(1)(8)-(2)8 to get 8 for (d) sqrt((2*28)/3) which equals 4.32 for (e) sqrt((2*20)/3) which equals 3.65 for (f) sqrt((2*8)/3) which equals 2.30
Note: for a b and c units are Joules and d e f in in m/s
I just do not understand why these are wrong. Thanks for any help!