Adding mass when a blocks rests on another block?

[dantechiesa]

Homework Statement

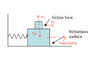
The figure shows a 1.0 kg mass riding on top of a 5.0 kg mass which is attached
to a spring. The 5.0 kg mass oscillates on a frictionless surface, and the spring constant
is k = 50 N/m. There is friction between the upper block and the lower block, and the
coefficient of static friction is 0.50.

a) As the amplitude of the motion is increased, there is a maximum amplitude for
which the upper block does not slip on the lower block. Explain why, and calculate
this amplitude.

Homework Equations

kx = Ffr

The Attempt at a Solution

Can someone explain to me - possibly through a FBD, why, when figuring out question a), the Ffr between the 2 blocks is 6.0kg * 9.8 * .50?

Why would it not be the normal force of the top box? Simply 1 * 9.8 * .5?

How does the larger bottom block exert a normal force up and why does this not happen with, let's say an object lying on the Earth (we don't include the mass of the earth)

Thanks.

 

[Charles Link]

The coefficient of static friction allows you to compute the maximum force that is available from static friction. If something is sitting still, the frictional force is zero, but if you push on the weight, or try to pull the rug out from under it, it will supply the necessary frictional force to oppose movement. There is an upper limit to this frictional force, given by the equation for static friction with the coefficient of static friction.

 

[dantechiesa]

The coefficient of static friction allows you to compute the maximum force that is available from static friction. If something is sitting still, the frictional force is zero, but if you push on the weight, or try to pull the rug out from under it, it will supply the necessary frictional force to oppose movement. There is an upper limit to this frictional force, given by the equation for static friction with the coefficient of static friction.

Thanks for the reply,
how come I use the mass of the lower block when computing this friction force?

Wouldn't I simply use the normal force from the top block only?

 

[Charles Link]

Thanks for the reply,
how come I use the mass of the lower block when computing this friction force?

Wouldn't I simply use the normal force from the top block only?

Yes, from the top block only. $F_N=W=mg$.

 

[dantechiesa]

Yes, from the top block only. $F_N=W=mg$.

So computing the question a),
finding the distance at which the box begins to slip.
Would be at the point where force of the spring, kx = Ffr of the box

50 * x = .5 1.0 * 9.8

x = .098

However, the answer key states: as the amplitude increases, more force is required to accelerate the upper block in its SHM – eventually, the force required is larger than what (static) friction can provide, and the upper block will slip on the lower block. It does so when the amplitude of the SHM is A = 0.59

.59 is only found when the Ffr is found using: .5 * (1.0 + 5.0) * 9.8
adding the two boxes mass. Why?

 

[haruspex]

Would be at the point where force of the spring, kx = Ffr of the box

Why?

 

[dantechiesa]

Why?

Because once the force of static friction of the top box is overcome by the force of the spring, the box will begin to slide.

no?

 

[haruspex]

Because once the force of static friction of the top box is overcome by the force of the spring, the box will begin to slide.

no?

Different boxes. Draw a separate FBD for box.

 

[dantechiesa]

Different boxes. Draw a separate FBD for box.

After thinking about it some more, I am starting to really get lost.

Does the attached diagram look right?

Turns out i missed fg and fn of lower block. So pretend I have those in

 

[haruspex]

After thinking about it some more, I am starting to really get lost.

Does the attached diagram look right?

Turns out i missed fg and fn of lower block. So pretend I have those in

The diagram is right. Don't worry about vertical forces on the lower block - they will just balance out.
What is the maximum demand placed on the frictional force?

 

[dantechiesa]

The diagram is right. Don't worry about vertical forces on the lower block - they will just balance out.
What is the maximum demand placed on the frictional force?

I don't understand why it would not be equal to kx.

If the bottom box is 'shoved' forward by the spring by a force of kx, then as x gets larger and largr, the total force will.

The frictional force is only going to be able to withstand so much, and at a certain x, will be overcome.

What is flawed in my reasoning?

Thanks.

 

[haruspex]

I don't understand why it would not be equal to kx.

If the spring force and the frictional force on the lower box were in balance then the lower box would not accelerate. It does accelerate. The frictional force is therefore allowed to be less than the spring force.
The equation of relevance is ΣF=ma. Write out that equation for each box, on the assumption that there is no slipping.

 

[dantechiesa]

If the spring force and the frictional force on the lower box were in balance then the lower box would not accelerate. It does accelerate. The frictional force is therefore allowed to be less than the spring force.
The equation of relevance is ΣF=ma. Write out that equation for each box, on the assumption that there is no slipping.

Top box = 1.0 * a = Ffr
Bottom box = 5.0 * a = kx
Sorry but I am not seeing the relationship between the two (+ i don't think my fnet are right..)

 

[haruspex]

Bottom box = 5.0 * a = kx

You are missing a horizontal force. Remember - bodies exert equal and opposite forces on each other.

 

[dantechiesa]

You are missing a horizontal force. Remember - bodies exert equal and opposite forces on each other.

Ok, so since there is no friction on the bottom, the other surface the lower block is in contact with is the upper block.
So the Ffr between the 2 blocks also applies to the bottom box?
5.0 * a = kx +(?) ffr?

 

[haruspex]

+(?) ffr?

Equal and opposite

 

[dantechiesa]

Equal and opposite

Presuming you mean kx - Ffr = ma.

DOes that mean we now need to find a in order to find x?

Secondly, can you explain why its like that?

Thank you!

 

[haruspex]

DOes that mean we now need to find a in order to find x?

Yes, and your equation for the top box tells you the value of a.
The coefficient of friction sets a limit on the acceleration that can be achieved by the top box. If the lower box exceeds that then slipping will occur.

 

[dantechiesa]

Yes, and your equation for the top box tells you the value of a.
The coefficient of friction sets a limit on the acceleration that can be achieved by the top box. If the lower box exceeds that then slipping will occur.

It all worked,
Thanks for sticking it out!