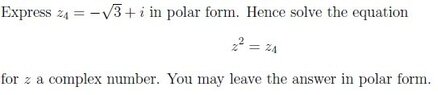TheFallen018 said:
Hi, I had a question I was working on a while back, and whilst I got the correct answer for it, I was told that there was a second solution to it that I missed.
Here is the question.
]
I worked my answer out to be sqrt(2)(cos(75)+i(sin(75))), however, it appears there is a second solution. From what I have gathered, it has to do with the fact that so long as the point remains in the same location of the graph, the solution is still equal. Therefore, it can crudely be expressed as sqrt(2)(cos(75(360x))+i(sin(75(360x)))), where x is an integer. However, that's still not the solution I'm looking for.
If anyone would be able to help clear this up, I would be most grateful.
You're doing complex numbers, by now you should be using radian measure.
$\displaystyle \begin{align*} z_4 &= -\sqrt{3} + \mathrm{i} \end{align*}$
This is in the second quadrant. $\displaystyle \begin{align*} \left| z_4 \right| = \sqrt{\left( \sqrt{3} \right) ^2 + 1^2} = \sqrt{4} = 2 \end{align*}$ and $\displaystyle \begin{align*} \textrm{Arg}\,\left( z_4 \right) = \pi - \arctan{ \left( \frac{1}{\sqrt{3}} \right) } = \pi - \frac{\pi}{6} = \frac{5\,\pi}{6} \end{align*}$. But every rotation of $\displaystyle \begin{align*} 2\,\pi \end{align*}$ units ends up back at the same point, so we can write
$\displaystyle \begin{align*} z_4 &= 2\,\mathrm{e}^{ \left( \frac{5\,\pi}{6} + 2\,\pi\,n \right) \, \mathrm{i} } \textrm{ where } n \in \mathbf{Z} \end{align*}$
Now when we solve $\displaystyle \begin{align*} z^2 = z_4 \end{align*}$ we have
$\displaystyle \begin{align*} z^2 &= 2\,\mathrm{e}^{\left( \frac{5\,\pi}{6} + 2\,\pi\,n \right) \,\mathrm{i}} \\ z &= \left[ 2\,\mathrm{e}^{\left( \frac{5\,\pi}{6} + 2\,\pi\,n \right) \,\mathrm{i}} \right] ^{\frac{1}{2}} \\ z &= \sqrt{2}\,\mathrm{e}^{ \left( \frac{5\,\pi}{12} + \pi\,n \right) \,\mathrm{i} } \end{align*}$Since $\displaystyle \begin{align*} \textrm{Arg}\,\left( z \right) \in \left( -\pi, \pi \right] \end{align*}$ that means we have
$\displaystyle \begin{align*} z_1 &= \sqrt{2} \,\mathrm{e}^{\frac{5\,\pi}{12}\,\mathrm{i}} \\ &= \sqrt{2} \, \left[ \cos{ \left( \frac{5\,\pi}{12} \right) } + \mathrm{i} \sin{ \left( \frac{5\,\pi}{12} \right) } \right] \\ &= \sqrt{2} \,\left[ \cos{ \left( \frac{\pi}{6} + \frac{\pi}{4} \right) } + \mathrm{i} \sin{ \left( \frac{\pi}{6} + \frac{\pi}{4} \right) } \right] \\ &= \sqrt{2} \,\left\{ \cos{ \left( \frac{\pi}{6} \right) } \cos{ \left( \frac{\pi}{4} \right) } - \sin{ \left( \frac{\pi}{6} \right) } \sin{ \left( \frac{\pi}{4} \right) } + \mathrm{i}\,\left[ \sin{\left( \frac{\pi}{6} \right) } \cos{ \left( \frac{\pi}{4} \right) } + \cos{ \left( \frac{\pi}{6} \right) } \sin{ \left( \frac{\pi}{4} \right) } \right] \right\} \\ &= \sqrt{2}\,\left[ \frac{\sqrt{3}}{2} \cdot \frac{1}{\sqrt{2}} - \frac{1}{2} \cdot \frac{1}{\sqrt{2}} + \mathrm{i} \,\left( \frac{1}{2} \cdot \frac{1}{\sqrt{2}} + \frac{\sqrt{3}}{2} \cdot \frac{1}{\sqrt{2}} \right) \right] \\ &= \frac{\sqrt{3} - 1}{2} + \mathrm{i} \,\left( \frac{\sqrt{3} + 1}{2} \right) \end{align*}$
and
$\displaystyle \begin{align*} z_2 &= \sqrt{2}\,\mathrm{e}^{\left( \frac{5\,\pi}{12} - \pi \right) \,\mathrm{i}} \\ &= \sqrt{2}\,\mathrm{e}^{ -\frac{7\,\pi}{12}\,\mathrm{i} } \\ &= \sqrt{2}\,\left[ \cos{ \left( -\frac{7\,\pi}{12} \right) } + \mathrm{i}\sin{ \left( -\frac{7\,\pi}{12} \right) } \right] \\ &= \sqrt{2}\,\left[ \cos{ \left( -\frac{\pi}{4} - \frac{\pi}{3} \right) } + \mathrm{i}\sin{ \left( -\frac{\pi}{4} - \frac{\pi}{3} \right) } \right] \\ &= \sqrt{2}\,\left\{ \cos{ \left( -\frac{\pi}{4} \right) } \cos{ \left( \frac{\pi}{3} \right) } + \sin{ \left( -\frac{\pi}{4} \right) } \sin{ \left( \frac{\pi}{3} \right) } + \mathrm{i}\,\left[ \sin{\left( -\frac{\pi}{4} \right) } \cos{ \left( \frac{\pi}{3} \right) } - \cos{ \left( -\frac{\pi}{4} \right) } \sin{ \left( \frac{\pi}{3} \right) } \right] \right\} \\ &= \sqrt{2} \,\left[ \frac{1}{\sqrt{2}}\cdot \frac{1}{2} - \frac{1}{\sqrt{2}}\cdot \frac{\sqrt{3}}{2} + \mathrm{i}\,\left( -\frac{1}{\sqrt{2}} \cdot \frac{1}{2} - \frac{1}{\sqrt{2}}\cdot \frac{\sqrt{3}}{2} \right) \right] \\ &= \frac{1 - \sqrt{3}}{2} + \mathrm{i} \,\left( \frac{-1 - \sqrt{3}}{2} \right) \end{align*}$