Adiabatic compression of gas at two temperatures

[Kalus]

I have a system that looks like this:

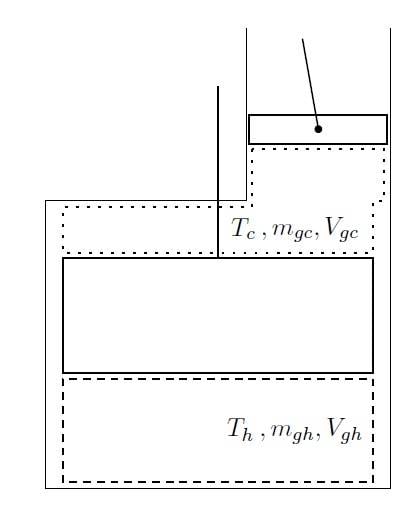
The top part is a piston, whereas the bottom is a displacer.

I have looked at the Isothermal case for this system in a separate thread (https://www.physicsforums.com/showthread.php?t=553165)

But in short, the result was that the pressure of the system is equal to:

$$m=m_{gc}+m_{gh}$$
$$P=\frac{mR}{V_{gc}/T_c +V_{gh}/T_h}$$

How can I modify this to take into account the temperature rise caused by adiabatic compression? I suppose I need to write the T_gc + T_gh as functions of the compression by the top piston, but how?

 

[Chestermiller]

Even if, as described in the linked thread, it is possible for the two chambers to exchange mass during compression (through a small gap surrounding the lower piston, so that the pressures are equalized at all times), when the system as described is compressed adiabatically, such exchange will not happen. Instead, both gas chambers will be compress by the same volume ratio at the overall volume:
$$\frac{V_c}{V_{c0}}=\frac{V_h}{V_{h0}}=\frac{V}{V_0}$$
Furthermore, the pressures in the two chambers will remain equal during the compression, and will vary as:
$$\frac{P}{P_0}=\left(\frac{V_0}{V}\right)^{\gamma}$$And the temperatues in the two chambers will vary as $$\frac{T_c}{T_{c0}}=\frac{T_h}{T_{h0}}=\left(\frac{V_0}{V}\right)^{\gamma-1}$$